题目内容
 已知二次函数y=kx2-(k+3)x+3在x=0和x=4时的函数值相等.
已知二次函数y=kx2-(k+3)x+3在x=0和x=4时的函数值相等.(1)求该二次函数的表达式;
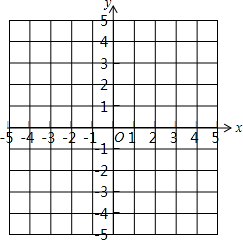
(2)画出该函数的图象,并结合图象直接写出当y<0时,自变量x的取值范围;
(3)已知关于x的一元二次方程k2x2-
| 3 |
考点:抛物线与x轴的交点,二次函数的图象,待定系数法求二次函数解析式
专题:计算题
分析:(1)利用x=0和x=4时的函数值相等得到16k-4(k+3)+3=3,解得k=1,于是得到二次函数解析式为y=x2-4x+3;
(2)先利用配方法得到抛物线的顶点坐标为(2,-1),再确定抛物线与x轴的交点坐标为(1,0)、(3,0),然后利用描点法画出抛物线,通过图象得到当1<x<3时,y<0;
(3)k=1时,方程化为x2-
mx+m2-m=0,再计算△=-(m-2)2+4,讨论:当-1≤m<0时,△<0;当m=0时,△=0;当0<m≤3时,△>0,然后根据判别式的意义判断根的情况.
(2)先利用配方法得到抛物线的顶点坐标为(2,-1),再确定抛物线与x轴的交点坐标为(1,0)、(3,0),然后利用描点法画出抛物线,通过图象得到当1<x<3时,y<0;
(3)k=1时,方程化为x2-
| 3 |
解答:解:(1)∵x=0和x=4时的函数值相等,
∴16k-4(k+3)+3=3,
∴k=1,
∴二次函数解析式为y=x2-4x+3;
(2)y=x2-4x+3=(x-2)2-1,则抛物线的顶点坐标为(2,-1),
当y=0时,x2-4x+3=0,解得x1=1,x2=3,则抛物线与x轴的交点坐标为(1,0)、(3,0),
如图,当1<x<3时,y<0;
(3)k=1时,方程化为x2-
mx+m2-m=0,
△=(-
m)2-4(m2-m)=-m2+4m=-(m-2)2+4,
当-1≤m<0时,△<0;
当m=0时,△=0;
当0<m≤3时,△>0,
∴当-1≤m<0时,原方程没有实数根;当m=0时,原方程有两个相等的实数根;当0<m≤3时,原方程有两个不相等的实数根.
∴16k-4(k+3)+3=3,

∴k=1,
∴二次函数解析式为y=x2-4x+3;
(2)y=x2-4x+3=(x-2)2-1,则抛物线的顶点坐标为(2,-1),
当y=0时,x2-4x+3=0,解得x1=1,x2=3,则抛物线与x轴的交点坐标为(1,0)、(3,0),
如图,当1<x<3时,y<0;
(3)k=1时,方程化为x2-
| 3 |
△=(-
| 3 |
当-1≤m<0时,△<0;
当m=0时,△=0;
当0<m≤3时,△>0,
∴当-1≤m<0时,原方程没有实数根;当m=0时,原方程有两个相等的实数根;当0<m≤3时,原方程有两个不相等的实数根.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目

 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,先从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的共有
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,先从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的共有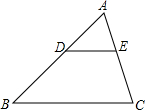 如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=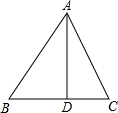 如图,在△ABC中,AD⊥BC,sinB=
如图,在△ABC中,AD⊥BC,sinB=