题目内容
已知:抛物线y=x2-2(m+2)x+m2-1与x轴有两个交点.
(1)求m的取值范围;
(2)当m为非正整数时,关于x的一元二次方程x2-2(m+2)x+m2-1有整数根,求m的值.
(1)求m的取值范围;
(2)当m为非正整数时,关于x的一元二次方程x2-2(m+2)x+m2-1有整数根,求m的值.
考点:抛物线与x轴的交点,根的判别式
专题:
分析:(1)抛物线与x轴有两个交点,则△=b2-4ac>0,从而求出m的取值范围.
(2)根据(1)求出m的值.然后将其代入关于x的一元二次方程x2-2(m+2)x+m2-1,通过解方程求得该方程的根,通过该方程的根是否是整数进行验证即可.
(2)根据(1)求出m的值.然后将其代入关于x的一元二次方程x2-2(m+2)x+m2-1,通过解方程求得该方程的根,通过该方程的根是否是整数进行验证即可.
解答:解:(1)∵抛物线y=x2-2(m+2)x+m2-1与x轴有两个交点,
∴△=b2-4ac>0,
即[-2(m+2)]2-4(m2-1)=16m+20>0,
解得m>-
,即m的取值范围是m>-
;
(2)由(1)知,m>-
.
∵m为非正整数,
∴m=0或m=-1.
①当m=0时,由原方程得到:y=x2-4x-1.
解得 x=2±
(不合题意).
则m=0不合题意;
②当m=-1时,由原方程得到:y=x2-2x=x(x-2).
解得 x1=0,x2=2,
0和2都是整数,
则m=-1符合题意.
综上所述,m的值是-1.
∴△=b2-4ac>0,
即[-2(m+2)]2-4(m2-1)=16m+20>0,
解得m>-
| 5 |
| 4 |
| 5 |
| 4 |
(2)由(1)知,m>-
| 5 |
| 4 |
∵m为非正整数,
∴m=0或m=-1.
①当m=0时,由原方程得到:y=x2-4x-1.
解得 x=2±
| 5 |
则m=0不合题意;
②当m=-1时,由原方程得到:y=x2-2x=x(x-2).
解得 x1=0,x2=2,
0和2都是整数,
则m=-1符合题意.
综上所述,m的值是-1.
点评:本题考查了抛物线与x轴的交点问题,注:①抛物线与x轴有两个交点,则△>0;②抛物线与x轴无交点,则△<0;③抛物线与x轴有一个交点,则△=0.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
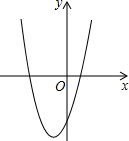 如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )
如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )| A、a>0,c>0 |
| B、a<0,c>0 |
| C、a>0,c<0 |
| D、a<0,c<0 |

 某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为50米的篱笆围成.已知墙长为26米(如图所示),设这个苗圃园平行于墙的一边的长为x米.
某中学课外活动小组准备围建一个矩形生物苗圃园,其中一边靠墙,另外三边用长为50米的篱笆围成.已知墙长为26米(如图所示),设这个苗圃园平行于墙的一边的长为x米.
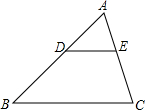 如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=