题目内容
 如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第6个菱形的边长为
如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第6个菱形的边长为考点:菱形的性质
专题:规律型
分析:根据已知和菱形的性质可分别求得AC,AC1,AC2的长,从而可发现规律,根据规律不难求得第6个菱形的边长.
解答: 解:连接DB,
解:连接DB,
∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=2,
∴BM=1,
∴AM=
=
,
∴AC=2AM=2
,
同理可得AC1=
AC=6,AC2=
AC1=6
,AC3=
AC2=18,AC4=
AC3=18
.
故答案为:18
.
 解:连接DB,
解:连接DB,∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=2,
∴BM=1,
∴AM=
| 22-12 |
| 3 |
∴AC=2AM=2
| 3 |
同理可得AC1=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
故答案为:18
| 3 |
点评:本题考查了菱形的性质,勾股定理,等边三角形的性质和判定的应用,解此题的关键是能根据求出的结果得出规律.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
一个扇形的圆心角为120°,半径为3,则这个扇形的面积为( )
| A、3π | B、9π | C、2π | D、4π |
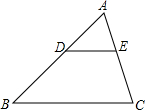 如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=
如图,在△ABC中,DE∥BC,DE与边AB相交于点D,与边AC相交于点E,如果AD=3,BD=4,AE=2,那么AC=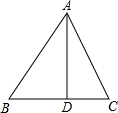 如图,在△ABC中,AD⊥BC,sinB=
如图,在△ABC中,AD⊥BC,sinB=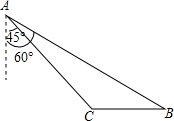 如图所示,2013年4月10日,中国渔民在中国南海huangyandao附近捕鱼作业,中国海监渔船在A第侦察发现,在东南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民.此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
如图所示,2013年4月10日,中国渔民在中国南海huangyandao附近捕鱼作业,中国海监渔船在A第侦察发现,在东南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民.此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(