题目内容
8.若4x2-5xy-6y2=0,其中xy≠0,则$\frac{x+y}{x-y}$的值为( )| A. | -3或$\frac{1}{7}$ | B. | 3或-$\frac{1}{7}$ | C. | 3 | D. | $\frac{1}{7}$ |
分析 先分解因式,即可求出x=-$\frac{3}{4}$y或x=2y,再分别代入求出即可.
解答 解:4x2-5xy-6y2=0,
(4x+3y)(x-2y)=0
4x+3y=0,x-2y=0
x=-$\frac{3}{4}$y.x=2y,
∵xy≠0,
∴当x=-$\frac{3}{4}$y时,$\frac{x+y}{x-y}$=-$\frac{1}{7}$,
当x=2y时,$\frac{x+y}{x-y}$=3,
故选B.
点评 本题考查了解一元二次方程的应用,能求出x=-$\frac{3}{4}$y或x=2y是解此题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
3.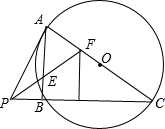 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )| A. | 10 | B. | 12 | C. | $5\sqrt{5}$ | D. | $5\sqrt{6}$ |
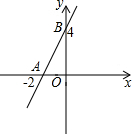 如图,直线y=kx+b交坐标轴于A,B两点,则不等式kx+b≤0的解集在数轴上表示正确的是( )
如图,直线y=kx+b交坐标轴于A,B两点,则不等式kx+b≤0的解集在数轴上表示正确的是( )

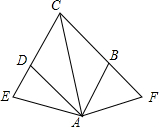 如图,点E.F分别是菱形ABCD的边CD与CB延长线上的点,且DE=BF,求证:∠E=∠F.
如图,点E.F分别是菱形ABCD的边CD与CB延长线上的点,且DE=BF,求证:∠E=∠F.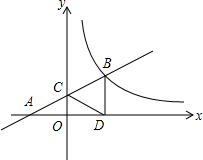 如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.
如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.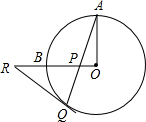 如图,OA、OB是⊙O的两条互相垂直的半径,P为OB上任一点,AP的延长线交⊙O于点Q,过点Q作⊙O的切线交OB的延长线于点R,求证:RP=RQ.
如图,OA、OB是⊙O的两条互相垂直的半径,P为OB上任一点,AP的延长线交⊙O于点Q,过点Q作⊙O的切线交OB的延长线于点R,求证:RP=RQ.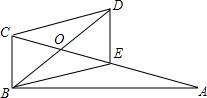 如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC的中点,BD平分∠ABC,求$\frac{OC}{OD}$的值.
如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC的中点,BD平分∠ABC,求$\frac{OC}{OD}$的值.