题目内容
3.苏宁电器商场计划用9万元从生产厂家购进50台电视机.已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.(1)若苏宁电器商场同时购进两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案.
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,你选择哪种方案?
分析 (1)本题的等量关系是:两种电视的台数和=50台,买两种电视花去的费用=9万元.然后分进的两种电视是A、B,A、C,B、C三种情况进行讨论.求出正确的方案;
(2)根据(1)得出的方案,分别计算出各方案的利润,然后判断出获利最多的方案.
解答 解:按购A,B两种,B,C两种,A,C两种电视机这三种方案分别计算,设购A种电视机x台,则B种电视机y台.
①当选购A,B两种电视机时,B种电视机购(50-x)台,可得方程:
1500x+2100(50-x)=90000,即5x+7(50-x)=300,
解得:x=25,
则B种电视机购50-25=25(台);
②当选购A,C两种电视机时,C种电视机购(50-x)台,可得方程:
1500x+2500(50-x)=90000,
解得:x=35,
则C种电视机购50-35=15(台);
③当购B,C两种电视机时,C种电视机为(50-y)台,可得方程:
2100y+2500(50-y)=90000,
解得:y=$\frac{175}{2}$,(不合题意,舍去)
由此可选择两种方案:一是购A,B两种电视机25台;二是购A种电视机35台,C种电视机15台.
(2)若选择(1)中的方案①,可获利150×25+250×15=8750(元),
若选择(1)中的方案②,可获利150×35+250×15=9000(元),
因为9000>8750,
所以为了获利最多,选择第二种方案.
点评 此题考查了一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系:两种电视的台数和=50台,买两种电视花去的费用=9万元.列出方程,再求解.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
11.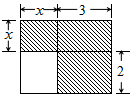 下面四个整式中,不能表示图中阴影部分面积的是( )
下面四个整式中,不能表示图中阴影部分面积的是( )
 下面四个整式中,不能表示图中阴影部分面积的是( )
下面四个整式中,不能表示图中阴影部分面积的是( )| A. | (x+3)(x+2)-2x | B. | x(x+3)+6 | C. | 3(x+2)+x2 | D. | x2+5x |
8.下列调查中,适宜采用全面调查方式的是( )
| A. | 了解一批圆珠笔的使用寿命 | |
| B. | 了解全国八年级学生身高的现状 | |
| C. | 检查发射神舟11号飞船的运载火箭的各零部件 | |
| D. | 考察世界人们保护海洋的意识 |
 如图,四边形ABCD为矩形,点E在AD边上,DE=4AE,EF∥AC,交CD边于点F,连接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,则线段EF的长为$\frac{24}{5}$.
如图,四边形ABCD为矩形,点E在AD边上,DE=4AE,EF∥AC,交CD边于点F,连接BE,若∠DEF=2∠ABE,BE=2$\sqrt{3}$,则线段EF的长为$\frac{24}{5}$.
 如图,⊙O的直径AB垂直于弦CD,垂足为P,BP=2cm,CD=6cm,求直径AB的长.
如图,⊙O的直径AB垂直于弦CD,垂足为P,BP=2cm,CD=6cm,求直径AB的长.
