题目内容
10.若关于x的一元二次方程ax2+bx+6=0的一个根为x=-2,则代数式6a-3b+6的值为( )| A. | 9 | B. | 3 | C. | 0 | D. | -3 |
分析 根据关于x的一元二次方程ax2+bx+6=0的一个根为x=-2,可以求得2a-b的值,从而可以求得6a-3b+6的值.
解答 解:∵关于x的一元二次方程ax2+bx+6=0的一个根为x=-2,
∴a×(-2)2+b×(-2)+6=0,
化简,得
2a-b+3=0,
∴2a-b=-3,
∴6a-3b=-9,
∴6a-3b+6=-9+6=-3,
故答案为:D.
点评 本题考查一元二次方程的解,解题的关键是明确题意,灵活变化,建立所求式子与已知方程之间的关系.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
1.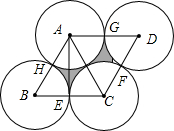 如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )
如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )
 如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )
如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )| A. | $\sqrt{3}$-π | B. | $\sqrt{3}$-2π | C. | 2$\sqrt{3}$-π | D. | 2$\sqrt{3}$-2π |
18.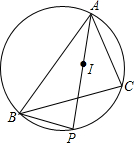 如图.已知△ABC的内切圆半径为1,外接圆半径为$\frac{5}{2}$,I是△ABC的内心,AI的延长线交△ABC的外接圆于点P,则IA•IP的值为( )
如图.已知△ABC的内切圆半径为1,外接圆半径为$\frac{5}{2}$,I是△ABC的内心,AI的延长线交△ABC的外接圆于点P,则IA•IP的值为( )
 如图.已知△ABC的内切圆半径为1,外接圆半径为$\frac{5}{2}$,I是△ABC的内心,AI的延长线交△ABC的外接圆于点P,则IA•IP的值为( )
如图.已知△ABC的内切圆半径为1,外接圆半径为$\frac{5}{2}$,I是△ABC的内心,AI的延长线交△ABC的外接圆于点P,则IA•IP的值为( )| A. | $\frac{5}{2}$ | B. | $\frac{25}{4}$ | C. | 5 | D. | $\frac{25}{2}$ |
5. 如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
 如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
如图,是某几何体的三视图及相关数据,则下面判断正确的是( )| A. | a>c | B. | b>c | C. | a2+4b2=c2 | D. | a2+b2=c2 |
15.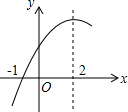 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
①4a+b=0;
②9a+c<3b;
③25a+5b+c=0;
④当x>2时,y随x的增大而减小.
其中正确的结论有( )
 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;
②9a+c<3b;
③25a+5b+c=0;
④当x>2时,y随x的增大而减小.
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
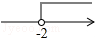
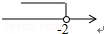
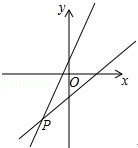 一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )
一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )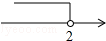

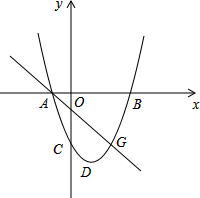 如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.
如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,与y轴交于点C,与x轴交于A、B两点,点A在原点的左侧,点B的坐标为(3,0),OB=OC=3OA.


