题目内容
19.如果关于x的方程ax2+4x-2=0有两个不相等的实数根,且关于x的分式方程$\frac{1}{2-x}$-$\frac{1-ax}{x-2}$=2有正数解,则符合条件的整数a的值是( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 先利用判别式的意义得到a≠0且△=42-4•a•(-2)>0,再解把分式方程化为整式方程得到x=-$\frac{2}{a-2}$,利用分式方程有正数解得到-$\frac{2}{a-2}$>0且-$\frac{2}{a-2}$≠2,然后求出几个不等式的公共部分,在此公共部分内确定整数a即可.
解答 解:∵方程ax2+4x-2=0有两个不相等的实数根,
∴a≠0且△=42-4•a•(-2)>0,解得a>-2且a≠0,
去分母得-1-(1-ax)=2(x-2),解得x=-$\frac{2}{a-2}$,
∵分式方程$\frac{1}{2-x}$-$\frac{1-ax}{x-2}$=2有正数解,
∴-$\frac{2}{a-2}$>0且-$\frac{2}{a-2}$≠2,解得a<2且a≠1,
∴a的范围为-2<a<2且a≠0,a≠1,
∴符合条件的整数a的值是-1.
故选A.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.也考查了分式方程的解.

练习册系列答案
相关题目
9.在△ABC中,∠A=50°,∠B=70°,则∠C的度数是( )
| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
10.若关于x的一元二次方程ax2+bx+6=0的一个根为x=-2,则代数式6a-3b+6的值为( )
| A. | 9 | B. | 3 | C. | 0 | D. | -3 |
11.若圆锥的底面半径为3,母线长为4,则这个圆锥的侧面积为 ( )
| A. | 12π | B. | 21π | C. | 24π | D. | 42π |
9.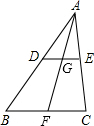 如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,F为BC边上一点,连接AF交DE于点G,下列说法不正确的是( )
如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,F为BC边上一点,连接AF交DE于点G,下列说法不正确的是( )
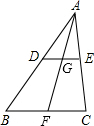 如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,F为BC边上一点,连接AF交DE于点G,下列说法不正确的是( )
如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,F为BC边上一点,连接AF交DE于点G,下列说法不正确的是( )| A. | $\frac{DG}{GE}$=$\frac{BF}{FC}$ | B. | $\frac{DG}{BF}$=$\frac{DE}{BC}$ | C. | $\frac{AD}{DB}$=$\frac{BF}{FC}$ | D. | $\frac{AD}{AE}$=$\frac{AB}{AC}$ |
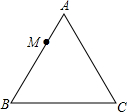 如图,点M从等边三角形的顶点A出发,沿直线匀速运动到点B,再沿直线匀速运动到点C,在整个过程中,设M与A的距离为y,点M的运动时间为x,那么y与x的图象大致为( )
如图,点M从等边三角形的顶点A出发,沿直线匀速运动到点B,再沿直线匀速运动到点C,在整个过程中,设M与A的距离为y,点M的运动时间为x,那么y与x的图象大致为( )