题目内容
18.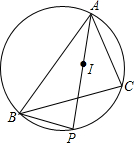 如图.已知△ABC的内切圆半径为1,外接圆半径为$\frac{5}{2}$,I是△ABC的内心,AI的延长线交△ABC的外接圆于点P,则IA•IP的值为( )
如图.已知△ABC的内切圆半径为1,外接圆半径为$\frac{5}{2}$,I是△ABC的内心,AI的延长线交△ABC的外接圆于点P,则IA•IP的值为( )| A. | $\frac{5}{2}$ | B. | $\frac{25}{4}$ | C. | 5 | D. | $\frac{25}{2}$ |
分析 设AP与BC交于点D,由点I是△ABC的内心可知,AI是△ABC的平分线,所以$\widehat{BP}=\widehat{CP}$,过点P作PG⊥BC于点G,并延长交△ABC的外接圆于点E,由垂径定理可知PE是△ABC外接圆的直径,所以∠EAP=90°,过点I作IF⊥BC于点F,易证△EAP∽△DFI,所以AP•DI=5,再证明BP=IP,然后利用△BDP∽△ABP得到$\frac{BD}{AB}=\frac{BP}{AP}$,再利用角平分线的性质可得$\frac{BD}{AB}=\frac{DI}{IA}$,所以IA•BP=AP•DI=5,即IA•IP=5.
解答 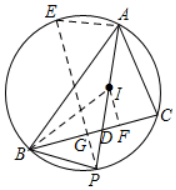 解:设AP与BC交于点D
解:设AP与BC交于点D
∵I是△ABC的内心,
∴AI平分∠BAC,
∴$\widehat{BP}=\widehat{CP}$,
过点P作PG⊥BC于点G,延长PG交△ABC的外接圆于点E,
∴由垂径定理可知PE是△ABC外接圆的直径,
∴PE=2×$\frac{5}{2}$=5,∠EAP=90°,
过点I作IF⊥BC于点F,
∴IF=1,
∵PE∥IF,
∴∠EPA=∠DIF,
∴△EAP∽△DFI,
∴$\frac{PE}{DI}=\frac{AP}{IF}$,
∴AP•DI=PE•IF=5,
连接BI,
∵$\widehat{BP}=\widehat{CP}$,
∴∠PBC=∠PAB,
∵BI平分∠ABC,
∴∠ABI=∠CBI,
∴∠PBC+∠CBI=∠ABI+∠PAB,
即∠PBI=∠PIB,
∴BP=IP
∵∠BPA=∠BPA,
∴△BDP∽△ABP,
∴$\frac{BD}{AB}=\frac{BP}{AP}$,
∵BI平分∠ABC,
∴$\frac{BD}{AB}=\frac{DI}{IA}$,
∴$\frac{DI}{IA}=\frac{BP}{AP}$,
∴IA•BP=AP•DI=5,
∵BP=IP,
∴IA•IP=5,
故选(C)
点评 本题考查三角形的外心与内心的性质,涉及角平分线的性质,垂径定理,相似三角形的性质与判定,等腰三角形的判定和性质等知识,内容较为综合,需要学生综合运用各种知识解决.

| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
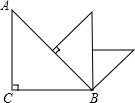 如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )
如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
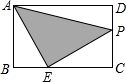 如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上一点,且BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路程长x之间的函数关系用图象表示应为( )
如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上一点,且BE=1,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路程长x之间的函数关系用图象表示应为( )| A. |  | B. |  | C. | 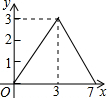 | D. | 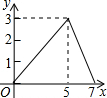 |
| A. | 9 | B. | 3 | C. | 0 | D. | -3 |
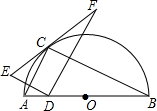 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论: