题目内容
1.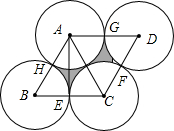 如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )
如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是( )| A. | $\sqrt{3}$-π | B. | $\sqrt{3}$-2π | C. | 2$\sqrt{3}$-π | D. | 2$\sqrt{3}$-2π |
分析 首先由题意可得△ABC是等边三角形,由菱形ABCD的边长为2,可求得菱形的高,以及各扇形的半径,继而求得菱形的面积与各扇形的面积的和,则可求得答案.
解答 解:根据题意得:AB=BC=AC,
∴∠B=60°,
∵菱形ABCD的边长为2,
∴AB=BC=2,
∵AE⊥BC,
∴BE=CE=$\frac{1}{2}$BC=1,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{3}$,
∴S菱形ABCD=BC•AE=2$\sqrt{3}$,S扇形AGH+S扇形BEH+S扇形CEF+S扇形DGF=$\frac{360×π×{1}^{2}}{360}$=π,
∴S阴影=2$\sqrt{3}$-π.
故选C.
点评 此题考查了菱形的性质以及扇形的面积的计算.注意将各扇形的面积和看作整体求解比较简单.

练习册系列答案
相关题目
12. 如图,在△ABC中,AD是∠BAC的角平分线,DE,DF分别是△ABD和△ACD的高,则AD与EF的关系是( )
如图,在△ABC中,AD是∠BAC的角平分线,DE,DF分别是△ABD和△ACD的高,则AD与EF的关系是( )
 如图,在△ABC中,AD是∠BAC的角平分线,DE,DF分别是△ABD和△ACD的高,则AD与EF的关系是( )
如图,在△ABC中,AD是∠BAC的角平分线,DE,DF分别是△ABD和△ACD的高,则AD与EF的关系是( )| A. | EF垂直平分AD | B. | AD垂直平分EF | ||
| C. | AD与EF互相垂直平分 | D. | 不能确定 |
9.在△ABC中,∠A=50°,∠B=70°,则∠C的度数是( )
| A. | 40° | B. | 60° | C. | 80° | D. | 100° |
16. 一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
 一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
6.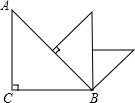 如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )
如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )
 如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )
如图,△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰Rt△,如此继续下去,直到所画直角三角形的斜边与△ABC的BC边在同一直线上时为止,此时,这个直角三角形的斜边长为( )| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
10.若关于x的一元二次方程ax2+bx+6=0的一个根为x=-2,则代数式6a-3b+6的值为( )
| A. | 9 | B. | 3 | C. | 0 | D. | -3 |
11.若圆锥的底面半径为3,母线长为4,则这个圆锥的侧面积为 ( )
| A. | 12π | B. | 21π | C. | 24π | D. | 42π |
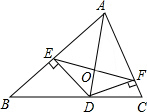 如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.