题目内容
13.计算:(1)$\frac{\sqrt{2}}{2}$($\sqrt{12}$+6$\sqrt{\frac{1}{27}}$-$\sqrt{48}$);
(2)已知x-1=$\sqrt{3}$,求代数式(x+1)2-4(x+1)+4的值.
分析 (1)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算;
(2)先利用完全平方公式得到原式=(x+1)2,然后利用整体代入的方法计算.
解答 解:(1)原式=$\frac{\sqrt{2}}{2}$(2$\sqrt{3}$+$\frac{2\sqrt{3}}{3}$-4$\sqrt{3}$)
=$\frac{\sqrt{2}}{2}$×(-$\frac{4\sqrt{3}}{3}$)
=-$\frac{2\sqrt{6}}{3}$;
(2)原式=[(x+1)-2]2=(x+1)2,
当x-1=$\sqrt{3}$时,原式=($\sqrt{3}$)2=3.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.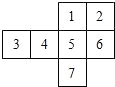 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )| A. | 1或2或3 | B. | 3或4或5 | C. | 4或5或6 | D. | 1或2或6 |
8. 如图,网格中小正方形的边长为1,点A、B为网格线的交点,则AB的长为( )
如图,网格中小正方形的边长为1,点A、B为网格线的交点,则AB的长为( )
 如图,网格中小正方形的边长为1,点A、B为网格线的交点,则AB的长为( )
如图,网格中小正方形的边长为1,点A、B为网格线的交点,则AB的长为( )| A. | 3 | B. | 5 | C. | 7 | D. | 12 |
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点. 如图,AC和BC相交于点O,OA=OC,OB=OD.求证:AB∥DC.
如图,AC和BC相交于点O,OA=OC,OB=OD.求证:AB∥DC.
 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB. 如图是从上面看一个由若干个相同的小正方体搭成的几何体得到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出从正面和左面看这个几何体得到的形状图.
如图是从上面看一个由若干个相同的小正方体搭成的几何体得到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出从正面和左面看这个几何体得到的形状图.