题目内容
18.已知:AB为⊙0的直径,CD、CF为⊙O的弦,AB⊥CD于点E,CF交AB于点G.(1)如图1,连接OD、OF、DG,求证:∠DOF=∠DGF;
(2)如图2,过点C作⊙O的切线,交BA的延长线于点H,点M在弧BC上,连接 CM、OM,若∠H=∠M,∠BGF=30°,求证:CM=CG;
(3)如图3,在(2)的条件下,连接FM(FM<CM),若FG=CE=4,求FM的长.

分析 (1)如图1,由直径AB垂直于点CD,利用垂径定理得到CE=DE,进而确定出CG=DG,利用等边对等角,圆周角定理,及外角性质,等量代换即可得证;
(2)如图2,连接OC,过O作OK⊥CM,利用垂径定理得到CK=MK,在直角三角形CEG中,利用30度角所对的直角边等于斜边的一半得到2CE=CG,由CH与圆相切,得到OC与CH垂直,利用同角的余角相等得到一对角相等,再由一对直角相等,OC=OC,得到三角形OCE与三角形OCK全等,利用全等三角形的对应边相等得到CK=CE,等量代换即可得证;
(3)如图3,过点O作ON⊥CF,则有CN=NF=$\frac{1}{2}$CF,由CG=2CE,求出CE长,利用锐角三角函数定义求出EG的长,进而求出ON与OG的长,以及OE的长,利用勾股定理求出CO的长,由三角形OEC与三角形OKC全等,得到对应角相等,进而求出RM的长,由FR-RM求出FM的长即可.
解答 (1)证明:如图1,
∵AB为圆O的直径,CD为圆O的弦,且AB⊥CD,
∴CE=DE,
∴GC=GD,
∴∠C=∠GDC,
∴∠DGF=∠C+∠GDC=2∠C,
∵∠DOF=2∠C,
∴∠DOF=∠DGF;
(2)证明:如图2,连接OC,过O作OK⊥CM,则有CK=KM=$\frac{1}{2}$CM,
在Rt△CEG中,∠CGE=∠BGF=30°,
∴CE=$\frac{1}{2}$CG,
∵CH与圆O相切,
∴OC⊥CH,
∴∠HCE+∠ECO=90°,
∵∠H+∠HCE=∠CEO=90°,
∴∠H=∠ECO=∠M,
∵OM=OC,
∴∠M=∠OCM=∠ECO,
∵OC=OC,∠OKC=∠OEC=90°,
∴△OKC≌△OEC,
∴CK=CE,
∴CM=CG;
(3)解:如图3,过点O作ON⊥CF,则有CN=NF=$\frac{1}{2}$CF,
∵FG=CE=4,
∴CG=2CE=8=CM,
在Rt△CEG中,tan∠CGE=$\frac{CE}{EG}$,即tan30°=$\frac{4}{EG}$,
∴EG=4$\sqrt{3}$,
在Rt△ONG中,NG=CG-CN=8-$\frac{1}{2}$×(8+4)=2,
∴ON=$\frac{2\sqrt{3}}{3}$,OG=$\frac{4\sqrt{3}}{3}$,
∴OE=4$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$,
在Rt△CEO中,CO=$\sqrt{C{E}^{2}+E{O}^{2}}$=$\frac{4\sqrt{21}}{3}$,
∴sin∠COE=$\frac{CE}{CO}$=$\frac{4}{\frac{4\sqrt{21}}{3}}$=$\frac{\sqrt{21}}{7}$,
∵OC=OM,OK⊥CM,
∴∠COK=$\frac{1}{2}$∠COM=∠F,
∵△OEC≌△OKC,
∴∠COE=∠COK=∠F,
过C作CR⊥FM,在Rt△CRF中,sinF=$\frac{CR}{CF}$=$\frac{CR}{12}$,
∵sin∠COE=$\frac{\sqrt{21}}{7}$,
∴CR=$\frac{12\sqrt{21}}{7}$,
∴FR=$\sqrt{C{F}^{2}-C{R}^{2}}$=$\frac{24\sqrt{7}}{7}$,
在Rt△CRM中,RM=$\sqrt{C{M}^{2}-C{R}^{2}}$=$\frac{4\sqrt{7}}{7}$,
则FM=FR-RM=$\frac{20\sqrt{7}}{7}$.
点评 此题属于圆综合题,涉及的知识有:垂径定理,圆周角定理,全等三角形的判定与性质,锐角三角函数定义,勾股定理,切线的性质,熟练掌握性质及定理是解本题的关键.

 如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1,3,则下列结论正确的个数有( )
如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1,3,则下列结论正确的个数有( )①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | x=1 | B. | x=-1 | C. | x=2 | D. | x=-2 |
 如图,梯形OABC中,BC∥AO,O(0,0),A(10,0),B(10,4),BC=2,G(t,0)是底边OA上的动点.
如图,梯形OABC中,BC∥AO,O(0,0),A(10,0),B(10,4),BC=2,G(t,0)是底边OA上的动点.
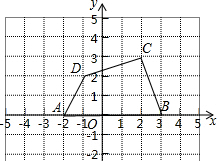 如图,四边形ABCD的各顶点的坐标分别为A(-2,0),B(3,0),C(2,4),D(-1,2).
如图,四边形ABCD的各顶点的坐标分别为A(-2,0),B(3,0),C(2,4),D(-1,2).