题目内容
17.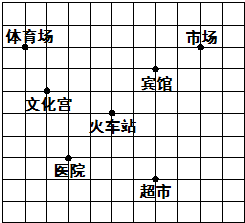 如图(小方格的边长为1),这是某市部分简图.
如图(小方格的边长为1),这是某市部分简图.(1)请你根据下列条件建立平面直角坐标系(在图中直接画出):①火车站为原点;②宾馆的坐标为(2,2).
(2)市场、超市的坐标分别为(4,3)、(2,-3);
(3)请将体育场、宾馆和火车站看作三点,用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,再画出平移后的△A′B′C′(在图中直接画出);
(4)根据坐标情况,求△ABC的面积.
分析 (1)利用火车站和宾馆的坐标画出直角坐标系;
(2)利用坐标系中各象限点的坐标特征写出市场、超市的坐标;
(3)把体育场、宾馆和火车站的横坐标不变,纵坐标减去4描出各点即可得到△A′B′C′;
(4)用矩形的面积分别减去三个三角形的面积求解.
解答 解:(1)如图, (2)市场的坐标为(4,3),超市的坐标为(2,-3);
(2)市场的坐标为(4,3),超市的坐标为(2,-3);
(3)如图;
(4)△ABC面积=3×6-$\frac{1}{2}$×2×2-$\frac{1}{2}$×4×3-$\frac{1}{2}$×1×6
=18-2-6-3
=7.
故答案为(4,3),(2,-3).
点评 本题考查了坐标确定位置:平面坐标系中的点与有序实数对一一对应;记住平面内特殊位置的点的坐标特征.会利用面积的和差计算不规则几何图形的面积.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
8.下列各式中正确的是( )
| A. | $\frac{x+y}{x+y}=0$ | B. | $\frac{y}{x}=\frac{{y}^{2}}{{x}^{2}}$ | C. | $\frac{-x+y}{-x-y}=1$ | D. | $\frac{1}{-x+y}=-\frac{1}{x-y}$ |
9.若关于x的一元二次方程ax2+3x+1=0有实数根,则a的取值范围( )
| A. | a<$\frac{9}{4}$ | B. | a≤$\frac{9}{4}$ | C. | a≥$\frac{9}{4}$ | D. | a≤$\frac{9}{4}$且a≠0 |
7.若把代数式x2-2x+3化为(x-m)2+k形式,其中m,k为常数,结果为( )
| A. | (x+1)2+4 | B. | (x-1)2+2 | C. | (x-1)2+4 | D. | (x+1)2+2 |
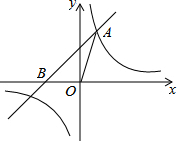 如图,已知在直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的一次函数y=x+b的图象交x轴于点B.
如图,已知在直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=$\frac{k}{x}$的图象上,过点A的一次函数y=x+b的图象交x轴于点B. 如图,已知AB∥CD,AE∥CF,请问∠BAE和∠DCF相等吗?试说明理由.
如图,已知AB∥CD,AE∥CF,请问∠BAE和∠DCF相等吗?试说明理由. 在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以$\sqrt{2}$cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒,则t=6秒时,S1=2S2.
在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,动点P从点A出发,沿A→D方向以$\sqrt{2}$cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒,则t=6秒时,S1=2S2.