题目内容
9.若关于x的一元二次方程ax2+3x+1=0有实数根,则a的取值范围( )| A. | a<$\frac{9}{4}$ | B. | a≤$\frac{9}{4}$ | C. | a≥$\frac{9}{4}$ | D. | a≤$\frac{9}{4}$且a≠0 |
分析 由关于x的一元二次方程ax2+3x+1=0有实数根,则a≠0,且△≥0,即△=32-4a=9-4a≥0,解不等式得到a的取值范围.
解答 解:∵关于x的一元二次方程ax2+3x+1=0有实数根,
∴a≠0,且△≥0,即△=32-4a=9-4a≥0,
解得a≤$\frac{9}{4}$,
∴a的取值范围为a≤$\frac{9}{4}$且a≠0,
故选D.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义和不等式的特殊解.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
19.下列分式变形中,正确的是( )
| A. | $\frac{a}{b}$=$\frac{a^2}{b^2}$ | B. | $\frac{a}{b}$=$\frac{ab}{ab}$ | C. | $\frac{a}{b}$=$\frac{a+2c}{b+2c}$(c≠0) | D. | $\frac{a}{b}$=$\frac{ac}{bc}$(c≠0) |
20.解方程.
(1)$\frac{10x}{2x-1}$+$\frac{5}{1-2x}$=2
(2)$\frac{1}{{x}^{2}+5x-6}$=$\frac{1}{{x}^{2}+x+6}$.
(1)$\frac{10x}{2x-1}$+$\frac{5}{1-2x}$=2
(2)$\frac{1}{{x}^{2}+5x-6}$=$\frac{1}{{x}^{2}+x+6}$.
1.$\sqrt{81}$的平方根是( )
| A. | 9 | B. | 3 | C. | ±9 | D. | ±3 |
18.下列说法正确的是( )
| A. | -1的平方根是-1 | |
| B. | 任何一个非负数的立方根都是非负数 | |
| C. | 如果一个数有平方根,那么这个数的平方根一定有两个 | |
| D. | 4的平方根是2 |
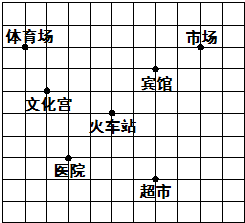 如图(小方格的边长为1),这是某市部分简图.
如图(小方格的边长为1),这是某市部分简图.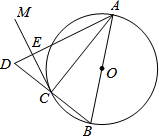 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.