Question

1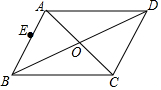．如图，四边形ABCD是平行四边形，E是AB边上一点，只用无刻度直尺在CD边上作点F，使得CF=AE．
（1）作出满足题意的点F，简要说明你的作图过程；
（2）依据你的作图，证明：CF=AE．

Answer 1

分析 （1）连接EO并延长交CD于F，则F为所求；
（2）根据平行四边形的性质得出AO=CO，AB∥CD，求出∠BAO=∠DCO，根据去三角形的判定得出△AOE≌△COF即可．

解答 解：（1）连接EO并延长交CD于F，则F点为所求；


（2）证明：∵ABCD为平行四边形，
∴AO=CO，AB∥CD，
∴∠BAO=∠DCO，
∵∠AOE=∠COF，
∴△AOE≌△COF，
∴AE=CF．

点评 本题考查了平行四边形的性质和全等三角形的性质和判定，能灵活运用平行四边形的性质进行推理是解此题的关键．