题目内容
4.化简$\sqrt{4{x}^{2}-4x+1}$-($\sqrt{(1-3x)}$)2 得( )| A. | x | B. | 5x-2 | C. | -x | D. | -5x+2 |
分析 根据二次根式的性质即可求出答案.
解答 解:∵1-3x≥0,
∴x≤$\frac{1}{3}$,
∴2x-1≤-$\frac{1}{3}$<0
∴原式=$\sqrt{(2x-1)^{2}}$+1-3x
=|2x-1|+1-3x
=-(2x-1)+1-3x
=-2x+1+1-3x
=-5x+2
故选(D)
点评 本题考查二次根式的性质,解题的关键是熟练运用二次根式的性质,本题属于基础题型.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
19.在2,-$\sqrt{2}$,-1,$\sqrt{3}$这四个实数中,最小的是( )
| A. | 2 | B. | -$\sqrt{2}$ | C. | -1 | D. | $\sqrt{3}$ |
14.为保护学生视力,课桌高度y(cm)与椅子高度x(xm)是按一次函数的关系配套设计的,如表是两套符合设计要求的课桌椅高度.
(1)求y与x之间的函数关系式;
(2)现有高78cm的课桌和高为43cm的椅子各一张,请说明它们是否配套.
| 第一套 | 第二套 | |
| 椅子高度x | 38 | 40 |
| 课桌高度y | 70 | 72 |
(2)现有高78cm的课桌和高为43cm的椅子各一张,请说明它们是否配套.
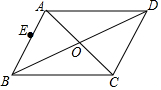 如图,四边形ABCD是平行四边形,E是AB边上一点,只用无刻度直尺在CD边上作点F,使得CF=AE.
如图,四边形ABCD是平行四边形,E是AB边上一点,只用无刻度直尺在CD边上作点F,使得CF=AE.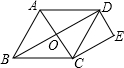 已知:如图,O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,DE、CE交于点E.
已知:如图,O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,DE、CE交于点E. 如图,四边形ABCD中,AD∥BC,∠C=132°,过点A作AE⊥BC,连接DE,若DE平分∠ADC,求∠AED的度数.
如图,四边形ABCD中,AD∥BC,∠C=132°,过点A作AE⊥BC,连接DE,若DE平分∠ADC,求∠AED的度数. 已知实数a,b在数轴上的位置如图所示,且|a|>|b|,化简$\sqrt{(a+b)^{2}}$-|a-b|.
已知实数a,b在数轴上的位置如图所示,且|a|>|b|,化简$\sqrt{(a+b)^{2}}$-|a-b|. 如图,在直角坐标平面内,△ABC的顶点A(-1,0),点B与点A关于原点对称,AB=BC,∠CAB=30°,将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,那么BE所在直线的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$.
如图,在直角坐标平面内,△ABC的顶点A(-1,0),点B与点A关于原点对称,AB=BC,∠CAB=30°,将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,那么BE所在直线的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$.