题目内容
10.解不等式组$\left\{\begin{array}{l}{x+2>0}\\{2(x-1)+3≥3x}\end{array}\right.$并判断x=-$\sqrt{3}$是否为该不等式组的解.分析 先分别求出各不等式的解集,再求出其公共解集,判断出-$\sqrt{3}$是否在此不等式组解集范围内即可.
解答 解:$\left\{\begin{array}{l}{x+2>0①}\\{2(x-1)+3≥3x②}\end{array}\right.$,
由①得x>-2,
由②得x≤1,
∴原不等式组的解集是-2<x≤1.
∵-2<-$\sqrt{3}$≤1,
∴x=-$\sqrt{3}$是该不等式组的解.
点评 本题考查的是解一元一次不等式组,能根据解不等式组的法则求出该不等式组的解集是解答此题的关键.

练习册系列答案
相关题目
19.在2,-$\sqrt{2}$,-1,$\sqrt{3}$这四个实数中,最小的是( )
| A. | 2 | B. | -$\sqrt{2}$ | C. | -1 | D. | $\sqrt{3}$ |
 如图,四边形ABCD是平行四边形,E是AB边上一点,只用无刻度直尺在CD边上作点F,使得CF=AE.
如图,四边形ABCD是平行四边形,E是AB边上一点,只用无刻度直尺在CD边上作点F,使得CF=AE.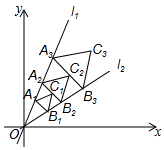 如图,点A1(1,$\sqrt{3}}$)在直线l1:y=$\sqrt{3}$x上,过点A1作A1B1⊥l1交直线l2:y=$\frac{{\sqrt{3}}}{3}$x于点B1,以A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第n个等边三角形AnBnCn的面积为$\frac{\sqrt{3}}{2}$$(\frac{3}{2})^{2n-3}$.(用含n的代数式表示)
如图,点A1(1,$\sqrt{3}}$)在直线l1:y=$\sqrt{3}$x上,过点A1作A1B1⊥l1交直线l2:y=$\frac{{\sqrt{3}}}{3}$x于点B1,以A1B1为边在△OA1B1外侧作等边三角形A1B1C1,再过点C1作A2B2⊥l1,分别交直线l1和l2于A2,B2两点,以A2B2为边在△OA2B2外侧作等边三角形A2B2C2,…按此规律进行下去,则第n个等边三角形AnBnCn的面积为$\frac{\sqrt{3}}{2}$$(\frac{3}{2})^{2n-3}$.(用含n的代数式表示) 如图,正方形ABCD的边长为4,点B的坐标为(3,1),AB∥x轴,AD∥y轴,则点D的坐标为(-1,5).
如图,正方形ABCD的边长为4,点B的坐标为(3,1),AB∥x轴,AD∥y轴,则点D的坐标为(-1,5).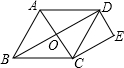 已知:如图,O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,DE、CE交于点E.
已知:如图,O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,DE、CE交于点E. 如图,在直角坐标平面内,△ABC的顶点A(-1,0),点B与点A关于原点对称,AB=BC,∠CAB=30°,将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,那么BE所在直线的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$.
如图,在直角坐标平面内,△ABC的顶点A(-1,0),点B与点A关于原点对称,AB=BC,∠CAB=30°,将△ABC绕点C旋转,使点A落在x轴上的点D处,点B落在点E处,那么BE所在直线的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$.