题目内容
13.试判断以如下的a、b、c为边长的三角形是不是直角三角形?(1)a=12,b=5,c=13;(是直角三角形)
(2)a=12,b=16,c=20;(是直角三角形)
(3)a=5,b=6,c=8;(不是直角三角形)
(4)a=$\sqrt{2}$,b=$\sqrt{7}$,c=3;(是直角三角形)
(5)a=$\sqrt{7}$,b=$\sqrt{15}$,c=$\sqrt{22}$;(是直角三角形)
分析 根据勾股定理的逆定理可知,当三角形中三边的关系为:a2+b2=c2时,则三角形为直角三角形.
解答 解:(1)52+122=132,符合勾股定理的逆定理,能组成直角三角形;
(2)122+162=202,符合勾股定理的逆定理,能组成直角三角形;
(3)52+62≠82,不符合勾股定理的逆定理,不能组成直角三角;
(4)$\sqrt{2}$2+$\sqrt{7}$2=32,符合勾股定理的逆定理,能组成直角三角形;
(5)$\sqrt{7}$2+$\sqrt{15}$2=$\sqrt{22}$2,符合勾股定理的逆定理,能组成直角三角形;
故答案为:是直角三角形;是直角三角形;不是直角三角形;是直角三角形;是直角三角形.
点评 此题考查的知识点是勾股数,解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足:a2+b2=c2时,则三角形ABC是直角三角形.解答时,只需看两较小数的平方和是否等于最大数的平方.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | a5+a5=a10 | B. | a6×a4=a24 | C. | 2-1÷20=2 | D. | a4-a4=0 |
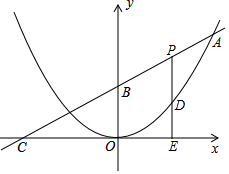 如图,已知二次函数图象的顶点在原点,直线y=$\frac{1}{2}$x+4的图象与该二次函数的图象交于点A(m,8),直线与x轴的交点为C,与y轴的交点为B.
如图,已知二次函数图象的顶点在原点,直线y=$\frac{1}{2}$x+4的图象与该二次函数的图象交于点A(m,8),直线与x轴的交点为C,与y轴的交点为B. 如图,在△ABC中,D是AB上一点,连接CD,请你添加一个适当的条件∠ADC=∠ACB,使△ABC∽△ACD.
如图,在△ABC中,D是AB上一点,连接CD,请你添加一个适当的条件∠ADC=∠ACB,使△ABC∽△ACD. 如图,已知矩形纸板面积为8a,两邻边之比为3:4,现欲在每个角处裁下一个面积为a的正方形后,制成一个无盖的纸箱.求制成的纸箱的侧面积.
如图,已知矩形纸板面积为8a,两邻边之比为3:4,现欲在每个角处裁下一个面积为a的正方形后,制成一个无盖的纸箱.求制成的纸箱的侧面积.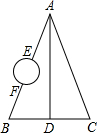 如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=DC=l km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km,则建造的斜拉桥长至少为1.1km.
如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=DC=l km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km,则建造的斜拉桥长至少为1.1km.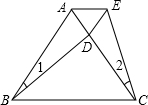 如图,△ABC是等边三角形,D为AC边上的一点,且∠1=∠2,BD=CE.
如图,△ABC是等边三角形,D为AC边上的一点,且∠1=∠2,BD=CE.