题目内容
1．
如图，A，B，C，D是四个村庄，B，D，C在一条东西走向公路的沿线上，BD=DC=l km，村庄AC，AD间也有公路相连，且公路AD是南北走向，AC=3km，只有AB之间由于间隔了一个小湖，所以无直接相连的公路．现决定在湖面上造一座斜拉桥，测得AE=1.2km，BF=0.7km，则建造的斜拉桥长至少为1.1km．
分析 首先证明△ABD≌△ACD，从而得到AB=AC=3km，然后依据EF=AB-AE-BF求解即可．
解答 解：∵由题意可知AD⊥BC，
∴∠ADB=∠ADC=90°．
在△ABD和△ACD中$\left\{\begin{array}{l}{AD=AD}\\{∠ADB=∠ADC}\\{BD=DC}\end{array}\right.$，
∴△ABD≌△ACD（SAS）．
∴AB=AC=3km．
∴EF=AB-AE-BF=3-1.2-0.7=1.1km．
故答案为：1.1．
点评 本题主要考查的是全等三角形的应用，证得△ABD≌△ACD是解题的关键．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
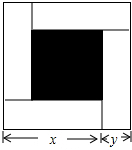如图，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个长方形的两边长（x＞y），观察图案，指出以下关系式：①x-y=n；②xy=$\frac{{m}^{2}-{n}^{2}}{4}$；③x2-y2=mn；④x2+y2=$\frac{{m}^{2}-{n}^{2}}{2}$．其中正确的关系式的有①②③．
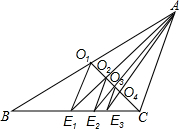如图，已知CO1是△ABC的中线，过点O1作O1E1∥AC交BC于点E1，连接AE1交CO1于点O2；过点O2作O2E2∥AC交BC于点E2，连接AE2交CO1于点O3；过点O3作O3E3∥AC交BC于点E3，…，如此继续，可以依次得到点O4，O5，…，On和点E4，E5，…，En．则OnEn=$\frac{1}{n+1}$AC．（用含n的代数式表示）
已知如图，AC=AE，AD=AB，∠ACB=∠DAB=90°，AE∥CB，AC、DE交于点F．
