题目内容
4. 如图,已知矩形纸板面积为8a,两邻边之比为3:4,现欲在每个角处裁下一个面积为a的正方形后,制成一个无盖的纸箱.求制成的纸箱的侧面积.
如图,已知矩形纸板面积为8a,两邻边之比为3:4,现欲在每个角处裁下一个面积为a的正方形后,制成一个无盖的纸箱.求制成的纸箱的侧面积.
分析 设矩形的长宽分别为4k,3k.根据已知条件先求出矩形的长宽,再根据侧面积公式计算即可.
解答 解:设矩形的长宽分别为4k,3k.
由题意12k2=8a,
∴k=$\frac{\sqrt{6a}}{3}$,
∴矩形的长为$\frac{4\sqrt{6a}}{3}$,宽为$\sqrt{6a}$,
∴纸箱的侧面积=2($\frac{4\sqrt{6a}}{3}-2\sqrt{a}$+$\sqrt{6a}$-2$\sqrt{a}$)•$\sqrt{a}$=$\frac{14\sqrt{6}-24}{3}a$.
点评 本题考查矩形的性质,长方体的侧面积、二次根式的化简等知识,解题的关键是理解题意,求出长方体的长宽高是解题的关键,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若圆的一条弦把圆分成度数比为1:3的两条弧,则该弦所对的圆心角度数是( )
| A. | 90° | B. | 45° | C. | 135° | D. | 45°或135° |
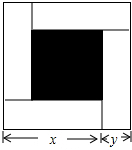 如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个长方形的两边长(x>y),观察图案,指出以下关系式:①x-y=n;②xy=$\frac{{m}^{2}-{n}^{2}}{4}$;③x2-y2=mn;④x2+y2=$\frac{{m}^{2}-{n}^{2}}{2}$.其中正确的关系式的有①②③.
如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个长方形的两边长(x>y),观察图案,指出以下关系式:①x-y=n;②xy=$\frac{{m}^{2}-{n}^{2}}{4}$;③x2-y2=mn;④x2+y2=$\frac{{m}^{2}-{n}^{2}}{2}$.其中正确的关系式的有①②③.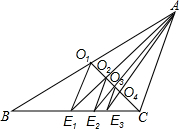 如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn=$\frac{1}{n+1}$AC.(用含n的代数式表示)
如图,已知CO1是△ABC的中线,过点O1作O1E1∥AC交BC于点E1,连接AE1交CO1于点O2;过点O2作O2E2∥AC交BC于点E2,连接AE2交CO1于点O3;过点O3作O3E3∥AC交BC于点E3,…,如此继续,可以依次得到点O4,O5,…,On和点E4,E5,…,En.则OnEn=$\frac{1}{n+1}$AC.(用含n的代数式表示) 已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.
已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.