题目内容
2.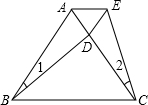 如图,△ABC是等边三角形,D为AC边上的一点,且∠1=∠2,BD=CE.
如图,△ABC是等边三角形,D为AC边上的一点,且∠1=∠2,BD=CE.(1)图中有全等的三角形吗?请找出来并证明;
(2)判断△ADE的形状,并说明理由.
分析 (1)△ABD和△ACE是全等三角形,利用SAS即可证明;
(2)根据△ABD≌△ACE得到AD=AE,∠CAE=∠BAD,即可判定出△ADE的形状.
解答 解:(1)∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠1=∠2}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE(SAS);
(2)△ADE是等边三角形
理由:∵△ABD≌△ACE,
∴AD=AE,∠CAE=∠BAD=60°,
∴△ADE是等边三角形.
点评 此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.解题要掌握SAS证明三角形全等,此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下面的图形是由边长为1的正方形按照某种规律排列而组成的.
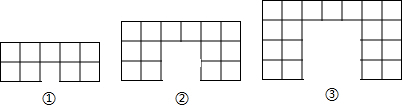
(1)观察图形,填写下表:
(2)推测第n个图形中,正方形的个数为5n+3,周长为10n+8(都用含n的代数式表示).
(3)写出第2016个图形的周长.

(1)观察图形,填写下表:
| 图形个数(n) | ① | ② | ③ |
| 正方形的个数 | 9 | 13 | 18 |
| 图形的周长 | 16 | 28 | 38 |
(3)写出第2016个图形的周长.
14.若圆的一条弦把圆分成度数比为1:3的两条弧,则该弦所对的圆心角度数是( )
| A. | 90° | B. | 45° | C. | 135° | D. | 45°或135° |
 已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.
已知如图,AC=AE,AD=AB,∠ACB=∠DAB=90°,AE∥CB,AC、DE交于点F.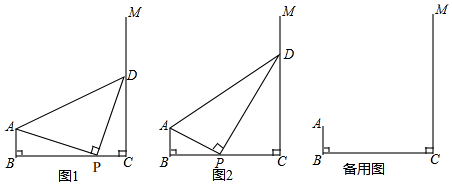
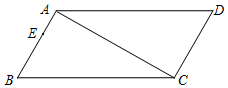 如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.
如图,在四边形ABCD中,∠B=∠D=60°,∠BAC=∠ACD=90°,点E为边AB上一点,AB=3AE=3cm,动点P从B点出发,以1cm/s的速度沿BC→CD→DA运动至A点停止,设运动时间为t秒.
 如图,用一个半径为30cm扇形铁皮,制作一个无底的圆锥(不计损耗),经测量圆锥的底面半径r为10cm,则扇形铁皮的面积为300πcm2.(结果保留π)
如图,用一个半径为30cm扇形铁皮,制作一个无底的圆锥(不计损耗),经测量圆锥的底面半径r为10cm,则扇形铁皮的面积为300πcm2.(结果保留π)