题目内容
2.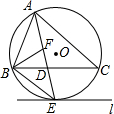 如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.(1)判断直线l与⊙O的位置关系,并说明理由;
(2)若∠ABC的平分线BF交AD于点F,求证:BE=EF.
分析 (1)作辅助线,连接半径,由角平分线得:∠BAE=∠CAE,圆周角相等,则弧相等,再由垂径定理证明OE⊥BC,所以OE⊥l,直线l与⊙O相切;
(2)证明∠EBF=∠EFB,根据等角对等边得结论.
解答 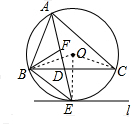 解:(1)直线l与⊙O相切,理由是:
解:(1)直线l与⊙O相切,理由是:
如图,连接OE、OB、OC,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴$\widehat{BE}$=$\widehat{CE}$,
∴∠BOE=∠COE,
∵OB=OC,
∴OE⊥BC,
∵l∥BC,
∴OE⊥l,
∴直线l与⊙O相切;
(2)∵BF平分∠ABC,
∴∠ABF=∠CBF,
∵∠CBE=∠CAE=∠BAE,
∴∠CBE+∠CBF=∠BAE+∠ABF,
∵∠EFB=∠BAE+∠ABF,
∴∠EBF=∠EFB,
∴BE=EF.
点评 本题考查了直线和圆的位置关系、垂径定理、等腰三角形的性质和判定以及圆心角、圆周角和弧的关系,熟练掌握切线的判定是关键:连接半径,证明半径与直线垂直.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
12. 如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则弦AB的长为( )
如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则弦AB的长为( )
 如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则弦AB的长为( )
如图,⊙O的半径为5,AB为⊙O的弦,OC⊥AB于点C.若OC=3,则弦AB的长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
14.若分式$\frac{x}{x-1}$有意义,则x的取值范围是( )
| A. | x>1 | B. | x=1 | C. | x<1 | D. | x≠1 |
 如图,直线m∥n,若∠1=140°,∠2=70°,求∠3的度数?
如图,直线m∥n,若∠1=140°,∠2=70°,求∠3的度数?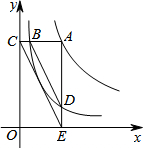 如图,已知反比例函数y1=$\frac{1}{x}$、y2=$\frac{4}{x}$在第一象限的图象,过y2上的任意一点A,作x轴的平行线交y1于B,交y轴于点C,过点A作x轴的垂线交y1于D,交x轴于点E,连接BD、CD,则$\frac{BD}{CE}$=$\frac{3}{4}$.
如图,已知反比例函数y1=$\frac{1}{x}$、y2=$\frac{4}{x}$在第一象限的图象,过y2上的任意一点A,作x轴的平行线交y1于B,交y轴于点C,过点A作x轴的垂线交y1于D,交x轴于点E,连接BD、CD,则$\frac{BD}{CE}$=$\frac{3}{4}$. 若一次函数y=kx+b图象如图,当y>0时,x的取值范围是x<-1.
若一次函数y=kx+b图象如图,当y>0时,x的取值范围是x<-1.