题目内容
9.已知命题“关于x的一元二次方程x2+bx+1=0,当b>0时必有实数解”,能说明这个命题是假命题的一个反例可以是( )| A. | b=-2 | B. | b=-1 | C. | b=1 | D. | b=2 |
分析 先根据判别式得到△=b2-4,在满足b<0的前提下,取b=-1得到△<0,根据判别式的意义得到方程没有实数解,于是b=-1可作为说明这个命题是假命题的一个反例.
解答 解:△=b2-4,由于当b=-1时,满足b<0,
而△<0,方程没有实数解,所以当b=-1时,
可说明这个命题是假命题.
故选B.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式;有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了根的判别式.

练习册系列答案
相关题目
20.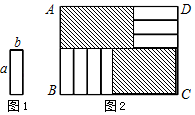 如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
 如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )
如图1,将7张长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )| A. | a=b | B. | a=3b | C. | a=2b | D. | a=4b |
4. 如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是( )
如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是( )
 如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是( )
如图,电路图上有四个开关A、B、C、D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
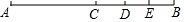 如图,已知线段AB=20,C是AB上的一点,D为CB上的一点,E为DB的中点,DE=3.
如图,已知线段AB=20,C是AB上的一点,D为CB上的一点,E为DB的中点,DE=3. 如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪CE的高度为1.5米,测得仰角α为36°,点E到电灯杆底端D的距离DE为4米,求路灯的高度AD是多少米(结果精确到0.01)?(参考数据:sin36°≈0.588,cos36°≈0.809,tan36°≈0.727)
如图,数学活动小组来到校园内的一盏路灯下测量路灯的高度,测角仪CE的高度为1.5米,测得仰角α为36°,点E到电灯杆底端D的距离DE为4米,求路灯的高度AD是多少米(结果精确到0.01)?(参考数据:sin36°≈0.588,cos36°≈0.809,tan36°≈0.727)