题目内容
1.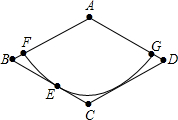 如图,纸片ABCD是一个菱形,其边长为2,∠BAD=120°.以点A为圆心的扇形与边BC相切于点E,与AB、AD分别相交于点F、G;
如图,纸片ABCD是一个菱形,其边长为2,∠BAD=120°.以点A为圆心的扇形与边BC相切于点E,与AB、AD分别相交于点F、G;(1)请你判断所作的扇形与边CD的位置关系,并说明理由;
(2)若以所作出的扇形为侧面围成一个圆锥,求该圆锥的全面积.
分析 (1)连接AE、AC,过点A作AH⊥CD,垂足为H,根据切线的性质得到AE⊥BC,根据菱形的性质得到AC平分∠BAD,由角平分线的性质得到AE=AH,于是结论可得;
(2)根据菱形的性质和等边三角形的性质求出AE的长,根据弧长公式求出$\widehat{FG}$的长,得到圆锥的侧面积,求出圆锥的底半径得到圆锥的底面积即可.
解答 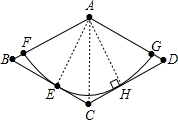 解:(1)相切;
解:(1)相切;
证明:连接AE、AC,过点A作AH⊥CD,垂足为H,
∵CB与⊙A相切,
∴AE⊥BC,
∵四边形ABCD为菱形,
∴AC平分∠BAD,
∴AE=AH,
∴扇形与边CD相切;
(2)∵四边形ABCD为菱形,∠BAD=120°,
∴△ABC是等边三角形,又其边长为2,
∴AE=$\sqrt{3}$,
∴$\widehat{FG}$的长为$\frac{120×π×\sqrt{3}}{180}$=$\frac{2\sqrt{3}}{3}$π,
则圆锥的侧面积为:$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$π×$\sqrt{3}$=π,
设圆锥的底半径为r,2πr=$\frac{2\sqrt{3}}{3}$π,
解得,r=$\frac{\sqrt{3}}{3}$,
则圆锥的底面积为:π×($\frac{\sqrt{3}}{3}$)2=$\frac{π}{3}$,
该圆锥的全面积=π+$\frac{π}{3}$=$\frac{4}{3}$π.
点评 本题考查的是菱形的性质、等边三角形的性质、扇形的弧长公式、扇形的面积公式,灵活运用相关定理和性质以及公式是解题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
12.如果式子m-7与4m-9互为相反数,则m的值为( )
| A. | $\frac{16}{3}$ | B. | -$\frac{16}{3}$ | C. | $\frac{16}{5}$ | D. | -$\frac{16}{5}$ |
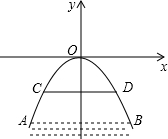 如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?
如图是以拱桥最高点为坐标原点,建立直角坐标系的抛物线拱桥.已知水在AB位置时,水面宽4$\sqrt{6}$米,水面距离桥顶12米.当水位上升达到警戒线CD时水面宽4$\sqrt{3}$米,若洪水到来时,水位以每小时0.6米速度上升.求水过警戒线后几小时淹到拱桥顶?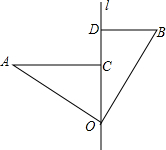 如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.若AC=10,BD=6,则CD=4.
如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.若AC=10,BD=6,则CD=4. 如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是旋转.
如图的组合图案可以看作是由一个正方形和正方形内通过一个“基本图案”半圆进行图形的“运动”变换而组成的,这个半圆的变换方式是旋转.