题目内容
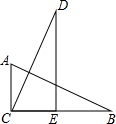 如图,在△ABC和△CDE中,若∠ACB=∠CED=90°,AB=CD,BC=DE,则下列结论中不正确的是( )
如图,在△ABC和△CDE中,若∠ACB=∠CED=90°,AB=CD,BC=DE,则下列结论中不正确的是( )| A、△ABC≌△CDE |
| B、CE=AC |
| C、AB⊥CD |
| D、E为BC中点 |
考点:全等三角形的判定与性质
专题:
分析:易证RT△ABC≌RT△CDE,可得CE=AC,∠A=∠DCE,即可求得∠DCE+∠B=90°,即可解题.
解答:解:在RT△ABC和RT△CDE中,
,
∴RT△ABC≌RT△CDE(HL),①正确;
∴CE=AC,②正确;
∠A=∠DCE,
∵∠A+∠B=90°,
∴∠DCE+∠B=90°,
∴AB⊥CD,③正确;
故选 D.
|
∴RT△ABC≌RT△CDE(HL),①正确;
∴CE=AC,②正确;
∠A=∠DCE,
∵∠A+∠B=90°,
∴∠DCE+∠B=90°,
∴AB⊥CD,③正确;
故选 D.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证RT△ABC≌RT△CDE是解题的关键.

练习册系列答案
相关题目
下列各式中,正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若关于x的多项式x2-2(m-3)x+16是完全平方式,则m的值为( )
| A、±7 | B、±1 |
| C、1或-7 | D、-1或7 |
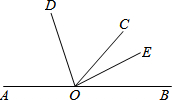 如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠AOD互余的角是( )
如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠AOD互余的角是( )| A、∠DOC |
| B、∠COE |
| C、∠COE与∠EOB |
| D、∠EOB |
 已知直线y=
已知直线y= 如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(EF)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(CD)1.6米,求旗杆的高度.
如图,某数学兴趣小组的同学利用标杆测量旗杆(AB)的高度:将一根5米高的标杆(EF)竖在某一位置,有一名同学站在一处与标杆、旗杆成一条直线,此时他看到标杆顶端与旗杆顶端重合,另外一名同学测得站立的同学离标杆3米,离旗杆30米.如果站立的同学的眼睛距地面(CD)1.6米,求旗杆的高度.