题目内容
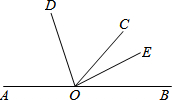 如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠AOD互余的角是( )
如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠AOD互余的角是( )| A、∠DOC |
| B、∠COE |
| C、∠COE与∠EOB |
| D、∠EOB |
考点:余角和补角,角平分线的定义
专题:
分析:根据角平分线的性质,可得∠AOD=∠COD,∠COE=∠BOE,再根据余角的定义求解即可.
解答:解:∵∠AOC+∠BOC=∠AOB=180°,
OD,OE分别是∠AOC和∠BOC的平分线,
∴∠DOC+∠COE=
(∠AOC+∠BOC)=90°.
∴∠AOD互余的角是∠COE与∠EOB.
故选C.
OD,OE分别是∠AOC和∠BOC的平分线,
∴∠DOC+∠COE=
| 1 |
| 2 |
∴∠AOD互余的角是∠COE与∠EOB.
故选C.
点评:本题考查了余角和补角及角平分线的定义,解答本题的关键是理解余角的定义,掌握角平分线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
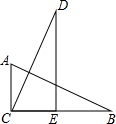 如图,在△ABC和△CDE中,若∠ACB=∠CED=90°,AB=CD,BC=DE,则下列结论中不正确的是( )
如图,在△ABC和△CDE中,若∠ACB=∠CED=90°,AB=CD,BC=DE,则下列结论中不正确的是( )| A、△ABC≌△CDE |
| B、CE=AC |
| C、AB⊥CD |
| D、E为BC中点 |
已知4个数:(-1)20015,|-2|,-(-5),π,-32,其中正数的个数有( )
| A、1 | B、2 | C、3 | D、4 |
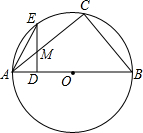 如图,AB是⊙O的直径,点C、E在
如图,AB是⊙O的直径,点C、E在