题目内容
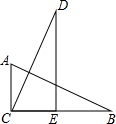
如图，某数学兴趣小组的同学利用标杆测量旗杆（AB）的高度：将一根5米高的标杆（EF）竖在某一位置，有一名同学站在一处与标杆、旗杆成一条直线，此时他看到标杆顶端与旗杆顶端重合，另外一名同学测得站立的同学离标杆3米，离旗杆30米．如果站立的同学的眼睛距地面（CD）1.6米，求旗杆的高度．考点：相似三角形的应用
专题：
分析：过点E作CG⊥AH于点H，交CD于点G得出△EGC∽△EHA，进而求出AH的长，进而求出AB的长．
解答：
解：过点E作CG⊥AH于点H，交CD于点G．
由题意可得 四边形EFDG、GDHB都是矩形，AB∥CD∥EF．
∴△AECG∽△EAH．
∴
=
．
由题意可得
EG=FD=3，GH=BD=30，CG=CD-GD=CD-EF=5-1.6=3.4．
∴
=
．
∴AH=34米．
∴AH=AH+HB=34+1.6=35.6米．
答：旗杆高ED为35.6米．
解：过点E作CG⊥AH于点H，交CD于点G．由题意可得 四边形EFDG、GDHB都是矩形，AB∥CD∥EF．
∴△AECG∽△EAH．
∴
| AH |
| CG |
| EH |
| EG |
由题意可得
EG=FD=3，GH=BD=30，CG=CD-GD=CD-EF=5-1.6=3.4．
∴
| AH |
| 3.4 |
| 30 |
| 3 |
∴AH=34米．
∴AH=AH+HB=34+1.6=35.6米．
答：旗杆高ED为35.6米．
点评：此题主要考查了相似三角形的应用，根据相似三角形判定得出△ECG∽△EAH是解题关键．
练习册系列答案
相关题目
如图，在△ABC和△CDE中，若∠ACB=∠CED=90°，AB=CD，BC=DE，则下列结论中不正确的是（ ）| A、△ABC≌△CDE |
| B、CE=AC |
| C、AB⊥CD |
| D、E为BC中点 |