题目内容
 已知直线y=
已知直线y=| 5 |
| 4 |
| 5 |
| 2 |
| 10 |
| x |
(1)求点B的坐标;
(2)求证:点C是线段AB的中点;
(3)求BD所对应的一次函数的解析式.
考点:反比例函数综合题
专题:
分析:(1)由直线y=
x+
和反比例函数y=
在第一象限的图象交于点B,可得方程组
,解此方程即可求得点B的坐标;
(2)首先由直线y=
x+
于点A,和y轴相交于点C,可求得点A与C的坐标,然后过点B作BE⊥x轴于E,则点E的坐标是(2,0),易得OC是△ABE的中位线,继而证得结论;
(3)易证得△ABE∽△BED,然后由相似三角形的对应边成比例,求得D的长,则可求得点D的坐标,然后利用待定系数法即可求得直线BD所对应的一次函数的解析式.
| 5 |
| 4 |
| 5 |
| 2 |
| 10 |
| x |
|
(2)首先由直线y=
| 5 |
| 4 |
| 5 |
| 2 |
(3)易证得△ABE∽△BED,然后由相似三角形的对应边成比例,求得D的长,则可求得点D的坐标,然后利用待定系数法即可求得直线BD所对应的一次函数的解析式.
解答:解:(1)由已知:
,
解得
,
(舍去),
∴点B的坐标是(2,5);
(2)∵直线y=
x+
于点A,和y轴相交于点C,
∴A、C两点的坐标分别是(-2,0),(0,
),
过点B作BE⊥x轴于E,则点E的坐标是(2,0),
∵A(-2,0),E(2,0),O(0,0),
∴OA=OE=2,
∴O是AE的中点,
又∵OC⊥AE,BE⊥AE,
∴OC∥BE,
∴OC是△ABE的中位线,
即C是AB的中点;
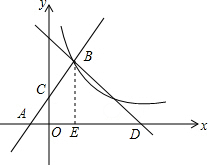 (3)在Rt△ABD中,BE⊥AD,
(3)在Rt△ABD中,BE⊥AD,
∴∠AEB=∠BED=90°,
∴∠BAE+∠ABE=90°,
∵∠ABD=90°,
∴∠ABE+∠EBD=90°,
∴∠BAE=∠EBD,
∴△ABE∽△BED,
∴AE:BE=BE:ED,
∴BE2=AE•ED,
又∵AE=4,BE=5
∴ED=
,
∴OD=2+
=
,
点D的坐标为(
,0),
设直线BD为y=kx+b,
则
,
解得:
,
∴BD的方程为:y=-
x+
.
|
解得
|
|
∴点B的坐标是(2,5);
(2)∵直线y=
| 5 |
| 4 |
| 5 |
| 2 |
∴A、C两点的坐标分别是(-2,0),(0,
| 5 |
| 2 |
过点B作BE⊥x轴于E,则点E的坐标是(2,0),
∵A(-2,0),E(2,0),O(0,0),
∴OA=OE=2,
∴O是AE的中点,
又∵OC⊥AE,BE⊥AE,
∴OC∥BE,
∴OC是△ABE的中位线,
即C是AB的中点;
 (3)在Rt△ABD中,BE⊥AD,
(3)在Rt△ABD中,BE⊥AD,∴∠AEB=∠BED=90°,
∴∠BAE+∠ABE=90°,
∵∠ABD=90°,
∴∠ABE+∠EBD=90°,
∴∠BAE=∠EBD,
∴△ABE∽△BED,
∴AE:BE=BE:ED,
∴BE2=AE•ED,
又∵AE=4,BE=5
∴ED=
| 25 |
| 4 |
∴OD=2+
| 25 |
| 4 |
| 33 |
| 4 |
点D的坐标为(
| 33 |
| 4 |
设直线BD为y=kx+b,
则
|
解得:
|
∴BD的方程为:y=-
| 4 |
| 5 |
| 33 |
| 5 |
点评:此题属于一次函数的综合题,考查了待定系数求一次函数解析式、相似三角形的判定与性质以及反比例函数与一次函数的交点问题.此题综合性较强,难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
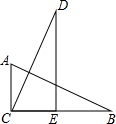 如图,在△ABC和△CDE中,若∠ACB=∠CED=90°,AB=CD,BC=DE,则下列结论中不正确的是( )
如图,在△ABC和△CDE中,若∠ACB=∠CED=90°,AB=CD,BC=DE,则下列结论中不正确的是( )| A、△ABC≌△CDE |
| B、CE=AC |
| C、AB⊥CD |
| D、E为BC中点 |
 如图△ABC中,∠A=62°,∠ACD=35°,∠ABE=20°,则∠BFD的度数是
如图△ABC中,∠A=62°,∠ACD=35°,∠ABE=20°,则∠BFD的度数是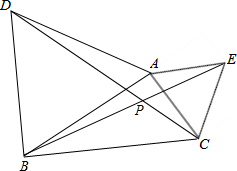 如图,△ABD,△AEC都是等边三角形.设BE,DC交于点P,连接AP,求式子
如图,△ABD,△AEC都是等边三角形.设BE,DC交于点P,连接AP,求式子