题目内容
8.2014年宁波市举行“足球迷”杯足球比赛,共有奇数个足球队参加,每个队都同其他队比赛一场,记分办法为胜一场得1分、平一场得0.5分,负一场得0分.已知其中有两队共得10分,其他队的平均分为整数,求参加此次比赛的足球队共有几支?分析 根据比赛场数乘以每场的得分,可得总得分,根据其他队的得分与两队得分的和也是总得分,可得方程,根据队数、得分数都是整数,可得答案.
解答 解:设参加此次比赛的足球队共有x支(x为正奇数),则全部比赛场次为$\frac{1}{2}$x(x-1),
∵每场得一分,
∴共得$\frac{1}{2}$x(x-1)分,
设其他队的平均分为y,(y为正整数),则总得分为10+y(x-2)
∴根据题意得,$\frac{1}{2}$x(x-1)=10+y(x-2),
∴y=$\frac{{x}^{2}-x-20}{2(x-2)}$=$\frac{{(x}^{2}-x-2)-18}{2(x-2)}$=$\frac{(x+1)(x-2)-18}{2(x-2)}$=$\frac{x+1}{2}$-$\frac{9}{x-2}$,
∵x为正奇数,
∴$\frac{x+1}{2}$为正整数,
∵y为正整数,
∴$\frac{9}{x-2}$是正整数,
∴(x-2)必须是9的因数,9的因数有1、3、9,
∴(x-2)可能为1、3、9,
∴x=3、5、11.
∵其中有两队共得10分,
∴$\frac{1}{2}$x(x-1)>10,
∴x2-x-20>0,
∴(x+4)(x-5)>0,
∴x>5或x<-4(舍),
∴x=11,
所以参加此次比赛的足球队共有11支.
点评 此题是应用类问题,主要考查了列方程,整数解,解一元二次不等式,因数,倍数,解本题的关键是根据题意列出方程,用x表示y之后处理成$\frac{x+1}{2}$-$\frac{9}{x-2}$是解本题的难点.

练习册系列答案
相关题目
10.若式子m$\sqrt{-\frac{1}{m}}$有意义,则化简此式等于( )
| A. | $\sqrt{m}$ | B. | $\sqrt{-m}$ | C. | -$\sqrt{m}$ | D. | -$\sqrt{-m}$ |
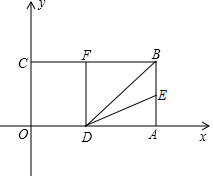 如图,以长方形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,连结BD,点A关于BD的对称点恰好落在线段BC边上的点F处.
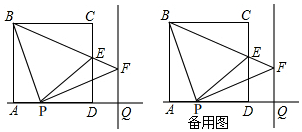
如图,以长方形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,连结BD,点A关于BD的对称点恰好落在线段BC边上的点F处. 已知:如图,AB=CD,AE⊥BC,DF⊥BC,CE=BF.
已知:如图,AB=CD,AE⊥BC,DF⊥BC,CE=BF.

 如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题:
如图,四边形ABCD中,AD=CD,AB=CB.我们把这种两组邻边分别相等的凸四边形叫做筝形.AC,BD叫作筝形的对角线.请你通过观察、测量、折纸等方法进行探究,并回答以下问题: