题目内容
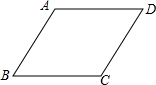
如图,在Rt△ABC中,∠B=90°,BC=4
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
| 3 |

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
考点:四边形综合题
专题:
分析:(1)利用已知用未知数表示出DF,AE的长,进而得出AE=DF;
(2)首先得出四边形AEFD为平行四边形,进而利用菱形的判定与性质得出AE=AD时,求出t的值,进而得出答案;
(3)利用①当∠EDF=90°时;②如图,当∠DEF=90°时;③当∠EFD=90°时,分别分析得出即可.
(2)首先得出四边形AEFD为平行四边形,进而利用菱形的判定与性质得出AE=AD时,求出t的值,进而得出答案;
(3)利用①当∠EDF=90°时;②如图,当∠DEF=90°时;③当∠EFD=90°时,分别分析得出即可.
解答:解:(1)∵在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t,
又∵AE=t
∴AE=DF;
(2)能,理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF,
又∵AE=DF,
∴四边形AEFD为平行四边形,
∵AB=BC×tan30°=4
×
=4,
∴AC=2AB=8,
∴AD=AC-DC=8-2t,
若使平行四边形AEFD为菱形,则需AE=AD,
即t=8-2t,
解得:t=
,
即当t=
时,四边形AEFD为菱形;
(3)①当∠EDF=90°时,四边形EBFD为矩形,
在Rt△AED中,∠ADE=∠C=30°,
∴AD=2AE,
即8-2t=2t,
解得:t=2;
②如图,当∠DEF=90°时,由(2)知,EF∥AD,
∴∠ADE=∠DEF=90°,
∵∠A=90°-∠C=60°,
∴AD=AE×cos60°,
即8-2t=
t,
解得:t=
;
③当∠EFD=90°时,此种情况不存在.
综上所述,当t=2或
时,△DEF为直角三角形.
∴DF=t,
又∵AE=t
∴AE=DF;
(2)能,理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF,
又∵AE=DF,
∴四边形AEFD为平行四边形,
∵AB=BC×tan30°=4
| 3 |
| ||
| 3 |
∴AC=2AB=8,
∴AD=AC-DC=8-2t,
若使平行四边形AEFD为菱形,则需AE=AD,
即t=8-2t,
解得:t=
| 8 |
| 3 |
即当t=
| 8 |
| 3 |
(3)①当∠EDF=90°时,四边形EBFD为矩形,
在Rt△AED中,∠ADE=∠C=30°,
∴AD=2AE,
即8-2t=2t,

解得:t=2;
②如图,当∠DEF=90°时,由(2)知,EF∥AD,
∴∠ADE=∠DEF=90°,
∵∠A=90°-∠C=60°,
∴AD=AE×cos60°,
即8-2t=
| 1 |
| 2 |
解得:t=
| 16 |
| 5 |
③当∠EFD=90°时,此种情况不存在.
综上所述,当t=2或
| 16 |
| 5 |
点评:此题主要考查了四边形综合以及菱形的判定和锐角三角函数的应用等知识,利用分类讨论得出是解题关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 如图,在菱形ABCD中,AB=m,∠ABC=α.将菱形ABCD绕点B顺时针旋转(旋转角小于90°),点A、C、D分别落在A′、C′、D′处,当A′C′⊥BC时,A′D=( )
如图,在菱形ABCD中,AB=m,∠ABC=α.将菱形ABCD绕点B顺时针旋转(旋转角小于90°),点A、C、D分别落在A′、C′、D′处,当A′C′⊥BC时,A′D=( )A、2mcos
| ||
B、2mcos
| ||
| C、2mcosα-m | ||
| D、2mcosα |
 如图,李明在大楼27米高(即PH=27米)的窗口P处进行观测,测得山坡上A处的俯角∠QPA=15°,山脚B处的俯角∠QPB=60°,已知该山坡的坡度i(即tan∠ABC)为1:
如图,李明在大楼27米高(即PH=27米)的窗口P处进行观测,测得山坡上A处的俯角∠QPA=15°,山脚B处的俯角∠QPB=60°,已知该山坡的坡度i(即tan∠ABC)为1: 用一根手指顶住一个平面图形内的某点,如果平面图形能保持平衡,那么这个点叫这个平面图形的重心,平行四边形的中心是对角线的交点,三角形的重心是三条中线的交点.请你用如图证明三角形的重心分一条中线成的两条线段的比为1:2,即在△ABC中,BE,CD是两条中线,它们交于G,求证:DG:CG=EG:BG=1:2.
用一根手指顶住一个平面图形内的某点,如果平面图形能保持平衡,那么这个点叫这个平面图形的重心,平行四边形的中心是对角线的交点,三角形的重心是三条中线的交点.请你用如图证明三角形的重心分一条中线成的两条线段的比为1:2,即在△ABC中,BE,CD是两条中线,它们交于G,求证:DG:CG=EG:BG=1:2. 甲、乙两名同学住在同一栋楼,在同一所中学读书,沿同一条路上学且途中要经过一个书报亭.某日,乙比甲早一点出发步行上学,甲骑自行车上学.下图表示甲、乙两人到书报亭的路程y甲、y乙(单位:米)与甲出发时间x(分)的函数图象,根据图象信息解答下列问题:
甲、乙两名同学住在同一栋楼,在同一所中学读书,沿同一条路上学且途中要经过一个书报亭.某日,乙比甲早一点出发步行上学,甲骑自行车上学.下图表示甲、乙两人到书报亭的路程y甲、y乙(单位:米)与甲出发时间x(分)的函数图象,根据图象信息解答下列问题: 如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5m,水面宽AB为8m,则水的最大深度CD为
如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果输水管的半径为5m,水面宽AB为8m,则水的最大深度CD为