题目内容
12.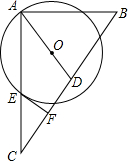 如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)
如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)
分析 先证明OE∥BC,再由EF⊥BC,证出EF⊥OE,即可证出EF是⊙O的切线.
解答 解:EF是⊙O的切线;理由如下:
连接OE,如图所示: ∵∠BAC=90°,D为BC上的中点,
∵∠BAC=90°,D为BC上的中点,
∴AD=$\frac{1}{2}$BC=CD,
∴∠C=∠DAC,
∵OA=OE,
∴∠DAC=∠AEO,
∴∠C=∠AEO,
∴OE∥BC,
∵EF⊥BC,
∴EF⊥OE,
∴EF是⊙O的切线;
故答案为:是.
点评 本题考查了切线的判定定理、平行线的判定以及直角三角形斜边上的中线性质;熟练掌握切线的判定定理,证明平行线是解决问题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
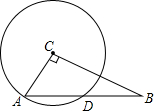 如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.
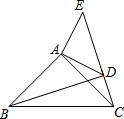 如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD,则∠BDE=90度.
如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD,则∠BDE=90度.