题目内容
20.解方程组:$\left\{\begin{array}{l}{4x+9y=12}\\{3y-2z=1}\\{7x+5z=\frac{19}{4}}\end{array}\right.$.分析 先①-②×3消去y后,得出4x+6z=9,再与7x+5z=$\frac{19}{4}$联立后,根据二元一次方程组解法解得即可.
解答 解:$\left\{\begin{array}{l}{4x+9y=12①}\\{3y-2z=1②}\\{7x+5z=\frac{19}{4}③}\end{array}\right.$,
①-②×3得:4x+6z=9④,
联立③④得:$\left\{\begin{array}{l}{4x+6z=9④}\\{7x+5z=\frac{19}{4}③}\end{array}\right.$,
④×7-③×4得:z=2,
把z=2代入②得:y=$\frac{5}{3}$,
把z=2代入③得:x=$-\frac{3}{4}$,
所以方程组的解是:$\left\{\begin{array}{l}{x=-\frac{3}{4}}\\{y=\frac{5}{3}}\\{z=2}\end{array}\right.$
点评 此题考查了三元一次方程组的解法.解三元一次方程组的关键是把“三元”转化为“二元”、把“二元”转化为“一元”,解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
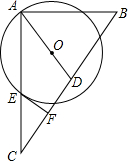 如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)
如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)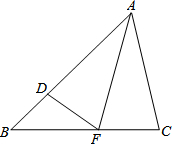 如图,在△ABC中,AB>AC,AF是∠BAC的平分线,D是AB上一点,AD=AC.
如图,在△ABC中,AB>AC,AF是∠BAC的平分线,D是AB上一点,AD=AC.