题目内容
7.【原题】如图1,在△ABC中,∠BAC的平分线与∠ABC的平分线交于点O,过点O作OD⊥AB,交AB于点D(BD>AD),求证:BC-AC=BD-AD.
【尝试探究】
在图1中过点O作OE⊥BC于点E,OF⊥AC于点F,连接OC,因为∠BAC的平分线与∠ABC的平分线交于点O,所以OD=OE=OF,所以CO是∠ACB的平分线,BD=所以利用全等三角形的性质可得BD=BE,AD=AF,CE=CF,所以BC-AC=BD-AD
【类比延伸】
如图2,在四边形ABCD中,各角的平分线交于点O,试判断AB,BC,CD,AD之间的数量关系,并加以证明.
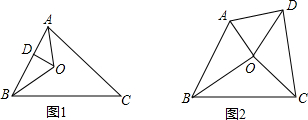
分析 尝试探究:过点O作OE⊥BC于E,OF⊥AC于F,连接OC,由角平分线的性质得到0D=OE=OF,根据全等三角形的性质得到结论;
类比延伸;.过O作OE⊥AB于E,OF⊥BC于F,OM⊥CD于M,ON⊥AD于N,由角平分线的性质得到OE=OF,根据全等三角形的性质得到BE=BF,CF=CM,DM=DN,AN=AE,于是得到AB+CD=AD+BC.
解答  解:尝试探究:如图1
解:尝试探究:如图1
过点O作OE⊥BC于E,OF⊥AC于F,连接OC,
∵OD⊥AB,∠BAC的平分线与∠ABC的平分线交于点O,
∴0D=OE=OF,CO是∠ACB的平分线,
在Rt△ADO与Rt△AFO中,
$\left\{\begin{array}{l}{OD=OF}\\{AO=AO}\end{array}\right.$,
∴Rt△ADO≌Rt△AFO(HL),
∴AD=AF,
同理BD=BE,CF=CE,
∴BC-AC=BE+CE-AF-CF=BE-AF=BD-AD;
类比延伸;AB+CD=AD+BC.
如图2过O作OE⊥AB于E,OF⊥BC于F,OM⊥CD于M,ON⊥AD于N,
∵BO平分∠ABC,
∴OE=OF,
在Rt△BOE与Rt△BOF中,
$\left\{\begin{array}{l}{OE=OF}\\{BO=BO}\end{array}\right.$,
Rt△BOE≌Rt△BOF(HL),
∴BE=BF,
同理CF=CM,DM=DN,AN=AE,
∴AB+CD=AE+BE+CM+DM,
AD+BC=AN+BF+CF+DN,
∴AB+CD=AD+BC.
点评 本题考查了角平分线的性质,全等三角形的判定与性质,等式的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
14.计算(-x-2y)2-(x-2y)2的结果是( )
| A. | -8xy | B. | -2x2-8y2 | C. | 8xy | D. | 4xy |
17. 如图,是一个平放在桌面上的瓷碗,它的主视图是( )
如图,是一个平放在桌面上的瓷碗,它的主视图是( )
 如图,是一个平放在桌面上的瓷碗,它的主视图是( )
如图,是一个平放在桌面上的瓷碗,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
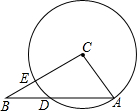 在△ABC中,∠B=30°,AC=10cm,BC=16cm,以点C为圆心,AC为半径的圆交AB于点D、交BC于点E.
在△ABC中,∠B=30°,AC=10cm,BC=16cm,以点C为圆心,AC为半径的圆交AB于点D、交BC于点E.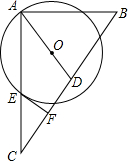 如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)
如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)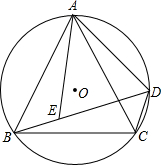 如图,△ABC内接于⊙O,AB=AC,D是弧AC上一点,连接BD,E是BD上一点,且BE=CD.
如图,△ABC内接于⊙O,AB=AC,D是弧AC上一点,连接BD,E是BD上一点,且BE=CD.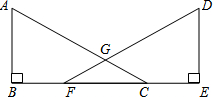 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证: