题目内容
16．已知：n是一个正整数，若$\sqrt{24n}$也是一个正整数，则n的最小值为6．分析 先把$\sqrt{24n}$=2$\sqrt{6n}$，从而判断出6n是完全平方数，所以得出答案正整数n的最小值是6．
解答 解：$\sqrt{24n}$=2$\sqrt{6n}$，则6n是完全平方数，
∴正整数n的最小值是6，
故答案为6
点评 本题考查了算术平方根，解题的关键是把$\sqrt{24n}$化为2$\sqrt{6n}$，从而判断出6n是完全平方数，然后解题就容易了．
练习册系列答案
相关题目
6．下列四个图形中，经过折叠可以围成一个棱柱的是（ ）
| A． |  | B． |  | C． |  | D． |  |
7．从1，2，3这三个数字中随机抽取两个，抽取的这两个数的和是奇数的概率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{5}{6}$ |
4．
如图，E，B，F，C四点在一条直线上，EB=FC，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（ ）
如图，E，B，F，C四点在一条直线上，EB=FC，∠A=∠D，再添一个条件仍不能证明△ABC≌△DEF的是（ ）| A． | AB=DE | B． | DF∥AC | C． | ∠E=∠ABC | D． | AB∥DE |
11．下列运算，正确的是（ ）
| A． | $\sqrt{20}$=2$\sqrt{10}$ | B． | $\sqrt{4}$-$\sqrt{2}$=$\sqrt{2}$ | C． | $\sqrt{（-3）^{2}}$=-3 | D． | $\sqrt{3}$•$\sqrt{2}$=$\sqrt{6}$ |
1．用配方法解一元二次方程x2-4x-1=0，配方后得到的方程是（ ）
| A． | （x-2）2=1 | B． | （x-2）2=4 | C． | （x-2）2=3 | D． | （x-2）2=5 |
8．如果规定向东行进为正，那么-50m表示的意义是（ ）
| A． | 向东行进50m | B． | 向南行进50m | C． | 向西行进50m | D． | 向北行进50m |
5．
从前有一天，一个笨汉拿着竹竿进屋，横拿竖拿都进不去，横着比门框宽4尺，竖着比门框高2尺．另一醉汉叫他沿着门的两个对角斜着拿竿，这个醉汉一试，不多不少刚好进去了，你知道竹竿有多长吗？若设竹竿的长为x尺，则下列方程，满足题意的是（ ）
从前有一天，一个笨汉拿着竹竿进屋，横拿竖拿都进不去，横着比门框宽4尺，竖着比门框高2尺．另一醉汉叫他沿着门的两个对角斜着拿竿，这个醉汉一试，不多不少刚好进去了，你知道竹竿有多长吗？若设竹竿的长为x尺，则下列方程，满足题意的是（ ）| A． | （x+2）2+（x-4）2=x2 | B． | （x+2）2+（x+4）2=x2 | C． | （x-2）2+（x-4）2=x2 | D． | （x-2）2+（x+4）2=x2 |
14．
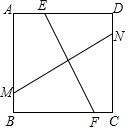如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分别在边AB、C D、A D、BC上．小明认为：若MN=EF，则MN⊥EF；小亮认为：若MN丄EF，则MN=EF，你认为（ ）
如图，正方形ABCD内有两条相交线段MN、EF，M、N、E、F分别在边AB、C D、A D、BC上．小明认为：若MN=EF，则MN⊥EF；小亮认为：若MN丄EF，则MN=EF，你认为（ ）| A． | 两人都对 | B． | 仅小亮对 | C． | 仅小明对 | D． | 两人都不对 |