题目内容
16.如图所示,要使△ABC∽△DEF,则x=40.
分析 由三边成比例得出两个三角形相似,即可得出结果.
解答 解:根据题意得:
当$\frac{EF}{BC}=\frac{DF}{AC}=\frac{DE}{AB}$时,△ABC∽△DEF,
即$\frac{x}{24}=\frac{25}{15}=\frac{20}{12}$,
解得:x=40.
答案为:40.
点评 本题考查了相似三角形的判定方法;熟记三边成比例的两个三角形相似是解决问题的关键.

练习册系列答案
相关题目
7.党的十八届三中全会决定提出研究制定渐进式延迟退休年龄政策.据报道,最近,人社部新闻发言人对延迟退休年龄进行了回应,称:每年只会延长几个月.
渐进式退休年龄应该怎么算?(假定2022年起实施延迟退休.)
以55岁退休为标准,假定每年延长退休时间为6个月,自方案实施起,逐年累计递增,直到达到新拟定的退休年龄.网友据此制作了一张“延迟退休对照表”.
(1)根据上表,1974年出生的人实际退休年龄将会是59岁;
(2)若每年延迟退休3个月,则2006年出生的人恰好是65岁退休;
(3)若1990年出生的人恰好是65岁退休,则每年延迟退休多少个月?
渐进式退休年龄应该怎么算?(假定2022年起实施延迟退休.)
以55岁退休为标准,假定每年延长退休时间为6个月,自方案实施起,逐年累计递增,直到达到新拟定的退休年龄.网友据此制作了一张“延迟退休对照表”.
| 出生年份 | 2022年年龄(岁) | 延迟退休时间(年) | 实际退休年龄(岁) |
| 1967 | 55 | 0.5 | 55.5 |
| 1968 | 54 | 1 | 56 |
| 1969 | 53 | 1.5 | 56.5 |
| 1970 | 52 | 2 | 57 |
| 1971 | 51 | 2.5 | 57.5 |
| 1972 | 50 | 3 | 58 |
| … | … | … | … |
(2)若每年延迟退休3个月,则2006年出生的人恰好是65岁退休;
(3)若1990年出生的人恰好是65岁退休,则每年延迟退休多少个月?
5.若|x|=3,则x-1的值为( )
| A. | 2 | B. | 4 | C. | -2或4 | D. | 2或-4 |
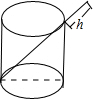 将一根26cm的筷子,置于底面直径为9cm,高12cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的最小值是11cm.
将一根26cm的筷子,置于底面直径为9cm,高12cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的最小值是11cm. 如图所示,由1开始连续自然数组成,观察规律,并完成以下各题.
如图所示,由1开始连续自然数组成,观察规律,并完成以下各题. 请你先在BC上找一点P,使点P到AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.
请你先在BC上找一点P,使点P到AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.