题目内容
6.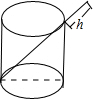 将一根26cm的筷子,置于底面直径为9cm,高12cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的最小值是11cm.
将一根26cm的筷子,置于底面直径为9cm,高12cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的最小值是11cm.
分析 筷子如图中所放的方式时,露在杯子外面的长度最小,在杯中的筷子与圆柱形水杯的底面直径和高构成了直角三角形,由勾股定理可求出筷子在水杯中的最大长度,筷子总长度减去杯子里面的长度即露在外面的最小长度.
解答  解:设杯子底面直径为a,高为b,筷子在杯中的最大长度为c,
解:设杯子底面直径为a,高为b,筷子在杯中的最大长度为c,
根据勾股定理,得:c2=a2+b2,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15(cm),
∴h的最小值=26-15=11(cm).
故答案为:11.
点评 本题考查了勾股定理的应用.熟练掌握勾股定理,善于观察题目的信息,由勾股定理求出c是解题的关键.

练习册系列答案
相关题目
18.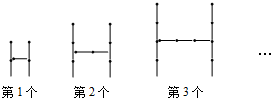 用火柴棍按如图所示的方式摆大小不同的“H”,依此规律,摆出第n个“H”需要火柴棍的根数是( )
用火柴棍按如图所示的方式摆大小不同的“H”,依此规律,摆出第n个“H”需要火柴棍的根数是( )
 用火柴棍按如图所示的方式摆大小不同的“H”,依此规律,摆出第n个“H”需要火柴棍的根数是( )
用火柴棍按如图所示的方式摆大小不同的“H”,依此规律,摆出第n个“H”需要火柴棍的根数是( )| A. | 2n+3 | B. | 3n+2 | C. | 3n+5 | D. | 4n+1 |
 如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)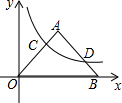 如图,双曲线y=$\frac{k}{x}$在第一象限内的图象与等腰直角三角形OAB相交于C点和D点,∠A=90°,OA=1,OC=2BD,则k的值是$\frac{8}{25}$.
如图,双曲线y=$\frac{k}{x}$在第一象限内的图象与等腰直角三角形OAB相交于C点和D点,∠A=90°,OA=1,OC=2BD,则k的值是$\frac{8}{25}$.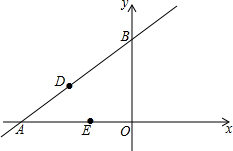 在平面直角坐标系xOy中,A(-8,0),B(0,6),点D、E同时从A点出发,其中点D沿射线AB运动,速度为每秒4个单位;点E沿射线AO运动,速度为每秒5个单位.
在平面直角坐标系xOy中,A(-8,0),B(0,6),点D、E同时从A点出发,其中点D沿射线AB运动,速度为每秒4个单位;点E沿射线AO运动,速度为每秒5个单位.
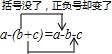 因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.
因此可以得到:括号前面是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变正负号.