题目内容
5.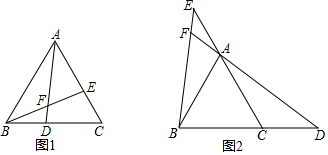 已知等边△ABC中,D,E分别是边BC,AC所在直线上的两点,且BD=CE,直线AD,BE交于点F.
已知等边△ABC中,D,E分别是边BC,AC所在直线上的两点,且BD=CE,直线AD,BE交于点F.(1)把下面的解答过程补充完整,并在括号内注明理由.
当点D,E分别在线段BC,AC上时(如图1)
①求证:AD=BE;②求∠AFE的度数;
①证明:∵△ABC是等边三角形(已知)
∴AB=AC(等边三角形的三条边都相等)
∠ABD=∠BCE(等边三角形的三个角都是60°)
∵BD=CE(已知)
∴△ABD≌△BCE(SAS)
∴AD=BE(全等三角形的对应边相等)
②解:由①得∠BAD=∠CBE(全等三角形的对应边相等)
∵∠AFB+∠BAD+∠ABF=180°(三角形的内角和等于180°)
∴∠AFB+∠CBE+∠ABF=180°(等量代换)
∵∠CBE+∠ABF=∠ABC=60°(等边三角形的三个角都是60°)
∴∠AFB=120°(等式的性质)
∵∠AFE+∠AFB=180°(平角的定义)
∴∠AFE=60°.
(2)当点D在线段BC的延长线上,点E在线段CA的延长线上时,如图2,
①求证:AD=BE;
②求∠AFE的度数.
分析 (1)①②只要证明△ABD≌△BCE即可解决问题;
(2)①②只要证明△ABD≌△BCE 即可解决问题;
解答 (1)①证明:∵△ABC是等边三角形(已知)
∴AB=BC(等边三角形的三条边都相等)
∴∠ABD=∠BCE(等边三角形的三个角都是60°)
∵BD=CE(已知)
∴△ABD≌△BCE(SAS)
∴AD=BE(全等三角形对应边相等)
故答案为AB=BC,∠ABD=∠BCE,SAS,全等三角形的对应边相等.
②解:由①得∠BAD=∠CBE(全等三角形的对应边相等)
∵∠AFB+∠BAD+∠ABF=180°(三角形的内角和等于180°)
∴∠AFB+∠CBE+∠ABF=180°(等量代换)
∵∠CBE+∠ABF=∠ABC=60°(已证)
∴∠AFB=120°(等式的性质)
∵∠AFE+∠AFB=180°(平角的定义)
∴∠AFE=60°
故答案为全等三角形对应边相等,三角形的内角和等于180°.
(2)①证明:∵△ABC是等边三角,
∴AB=BC,∠ABD=∠BCE,
∵BD=CE(已知),
∴△ABD≌△BCE,
∴AD=BE,
②∵△ABD≌△BCE
∴∠BAD=∠CBE,
∵∠D+∠BAD+∠ABD=180°,
∠D+∠CBE+∠AFB=180°,
∴∠ABD=∠AFB,
∵△ABC是等边三角形,
∴∠ABD=60°,
∴∠AFB=60°,
∵∠AFE+∠AFB=180°,
∴∠AFE=120°.
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
15.如果点A(m,n)、B(m-1,n-2)均在一次函数y=kx+b(k≠0)的图象上,那么k的值为( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
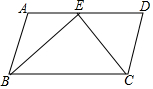 如图.已知四边形ABCD为平行四边形,AD=2AB,E为AD的中点,试说明BE与EC的位置关系.并说明理由.
如图.已知四边形ABCD为平行四边形,AD=2AB,E为AD的中点,试说明BE与EC的位置关系.并说明理由. 如图,在梯形ABCD中,AB∥CD,AD=BC=4,CD=2,AB=6,DM⊥AB,垂足为M,CN⊥AB,垂足为N,点P、Q分别是线段DM、CN上的动点,且DP=NQ,顺次联结AP、PQ、QB,设DP=t.
如图,在梯形ABCD中,AB∥CD,AD=BC=4,CD=2,AB=6,DM⊥AB,垂足为M,CN⊥AB,垂足为N,点P、Q分别是线段DM、CN上的动点,且DP=NQ,顺次联结AP、PQ、QB,设DP=t.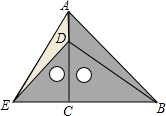 把等腰直角三角板ABC和等腰直角三角板ECD如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.
把等腰直角三角板ABC和等腰直角三角板ECD如图放置,点D在AC上,连接AE、BD,试判断AE与BD的关系,并说明理由.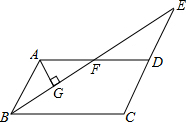 如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点.
如图,在平行四边形ABCD中,∠ABC的平分线与CD的延长线交于点E,与AD交于点F,且点F恰好为边AD的中点.