题目内容
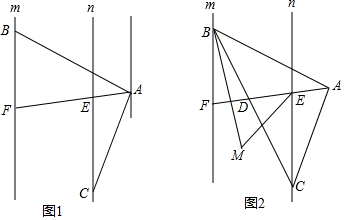
17.如图1,直线m∥n,点B、F在直线m上,点E、C在直线n上,连结FE并延长至点A,连结BA和CA,使∠AEC=∠BAC.(1)求证:∠BFA+∠BAC=180°;
(2)请在图1中找出与∠CAF相等的角,并加以证明;
(3)如图2,连结BC交AF于点D,作∠CBF和∠CEF的角平分线交于点M,若∠ADC=α,请直接写出∠M的度数(用含α的式子表示)
分析 (1)根据平行线的性质即可得到∠AEC=∠AFM,再根据∠AEC=∠BAC,可得∠AFM=∠BAC,根据∠BFA+∠AFM=180°,可得结论;
(2)根据三角形内角和定理以及平行线的性质,即可得到与∠CAF相等的角;
(3)过D作DF∥BF,过M作MG∥BF,根据平行线的性质,即可得到∠CED=∠FDE,∠FBD=∠FDB,再根据∠CBF和∠CEF的角平分线交于点M,可得∠CEM+∠FBM=$\frac{1}{2}$(∠CED+∠FBD),进而得到∠M的度数.
解答 解:(1)如图1,∵直线m∥n,
∴∠AEC=∠AFM,
∵∠AEC=∠BAC,
∴∠AFM=∠BAC,
又∵∠BFA+∠AFM=180°,
∴∠BFA+∠BAC=180°;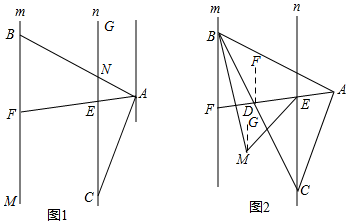
(2)与∠CAF相等的角有:∠ANC,∠ABF,∠BNG.
证明:∵∠AEC=∠BAC,∠ACE=∠NCA,
∴∠CAE=∠ANC=∠BNG,
∵m∥n,
∴∠ABF=∠ANC,
∴与∠CAF相等的角有:∠ANC,∠ABF,∠BNG;
(3)如图2,过D作DF∥BF,过M作MG∥BF,
∵BF∥CE,
∴DF∥BF∥CE,MG∥BF∥CE,
∴∠CED=∠FDE,∠FBD=∠FDB,
∴∠CED+∠FBD=∠EDB=180°-∠ADC=180°-α,
∵∠CBF和∠CEF的角平分线交于点M,
∴∠CEM+∠FBM=$\frac{1}{2}$(∠CED+∠FBD)=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,
∵MG∥BF∥CE,
∴∠CEM=∠GME,∠FBM=∠GMB,
∴∠BME=∠GME+∠GMB=∠CEM+∠FBM=90°-$\frac{1}{2}$α.
点评 本题主要考查了平行线的性质的运用,解决问题的关键是作辅助线构造内错角,解题时注意:两直线平行,内错角相等.

 阅读快车系列答案
阅读快车系列答案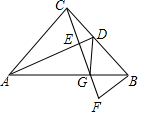 如图,在△ABC中,AC=BC,AC⊥BC,D为BC的中点,CF⊥AD于E,BF∥AC,证明:DG=FG.
如图,在△ABC中,AC=BC,AC⊥BC,D为BC的中点,CF⊥AD于E,BF∥AC,证明:DG=FG.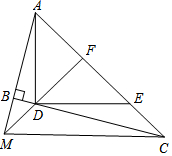 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M. 如图,AB为⊙O的直径,BC为⊙O的弦,过O点作OD⊥BC,交⊙O的切线CD于点D,交⊙O于点E,连接AC、AE,且AE与BC交于点F.
如图,AB为⊙O的直径,BC为⊙O的弦,过O点作OD⊥BC,交⊙O的切线CD于点D,交⊙O于点E,连接AC、AE,且AE与BC交于点F.