题目内容
解方程：
（1）2x2-10x=3
（2）2x（x-3）=9-3x．
（1）2x2-10x=3
（2）2x（x-3）=9-3x．
考点：解一元二次方程-因式分解法,解一元二次方程-公式法
专题：
分析：（1）根据配方法，可得方程的解；
（2）根据因式分解，可得方程的解．
（2）根据因式分解，可得方程的解．
解答：解：（1）系数化为1，得x2-5x=
，
配方，得x2-5x+
=
+
，
即（x-
）2=
，
解得x2=
，
x1=
；
（2）移项，得2x（x-3）+3（x-3）=0，
因式分解，得（x-3）（2x+3）=0．
x-3=0或2x+3=0．
解得x1=3，x2=-
．
| 3 |
| 2 |
配方，得x2-5x+
| 25 |
| 4 |
| 3 |
| 2 |
| 25 |
| 4 |
即（x-
| 5 |
| 2 |
| 31 |
| 4 |
解得x2=
5+
| ||
| 2 |
x1=
5-
| ||
| 2 |
（2）移项，得2x（x-3）+3（x-3）=0，
因式分解，得（x-3）（2x+3）=0．
x-3=0或2x+3=0．
解得x1=3，x2=-
| 3 |
| 2 |
点评：本题考查了解一元二次方程，因式分解法解方程时因式分解是解题关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
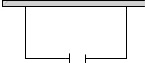如图，要建一个面积为140平方米的仓库，仓库的一边靠墙，这堵墙长16米，在与墙平行的一边，要开一扇2米宽的门．已知围建仓库的现有木板材料可使新建板墙的总长为32米，那么这个仓库设计的长和宽应分别为多少米？
如图，在Rt△ABC中，∠B=90°，AB=8cm，BC=6cm，点M，点N同时由A，C两点出发分别沿AB，CB方向向点B匀速移动，他们的速度都是1m/s．
如图，在△ABC中，∠ABC=60°，BC=12，AD是BC边上的高，E、F分别为边AB、AC的中点，当AD=6时，BC边上存在一点Q，使∠EQF=90°，求此时BQ的长．