题目内容

3．一只布袋内装有3个红球，6个黑球，1个白球（这些球除颜色外，其余没有区别），从中任意取出一球，则取得的球不是红球的概率是（　　）
A．$\frac{1}{3}$B．$\frac{3}{10}$C．$\frac{7}{10}$D．$\frac{1}{2}$

分析 根据条件可知3个红球，6个黑球，1个白球一共是10个，让不是红球的球的个数除以球的总数即为摸到不是红球的概率．

解答 解：因为3个红球，6个黑球，1个白球一共是10个，不是红球的有7个，
所以取得的球不是红球的概率是$\frac{7}{10}$．
故选C．

点评 本题考查了统计与概率中概率的求法，要认真阅读，明确：“不是红球的概率”．用到的知识点为：概率=所求情况数与总情况数之比．

练习册系列答案
相关题目
13．如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（　　）
A．5 cmB．10 cmC．20 cmD．40 cm
14．如图1，在正方形ABCD中，E、F分别为DC、BC边上的点，且满足∠EAF=45°，连结EF，试说明DE+BF=EF．
解：将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合．由旋转可得AB=ADMBGD，∠1=∠2，∠ABG=∠D=90°．
∴∠ABG+∠ABF=90°+90°=180°．
∴点G、B、F在同一条直线上．
∵∠EAF=45°，∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°
∵∠1=∠2，∴∠1+∠3=45°．
∴∠GAF=∠EAF．
又∵AG=AE，AF=AF．
∴△GAF≌△EAF．
∵GF=EF．
∴DE+BF=BG+BF=GF=EF．
（2）类比引申：
如图2，在四边形ABCD中，AB=AD，∠BAD=90°，点E、F分别在边BC、CD上，∠EAF=45°，若∠B、∠D都不是直角，则当∠B与∠D满足等量关系∠B+∠ADC=180°时，有EF=BE+DF．
（3）联想拓展
如图3，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°，试猜想BD、DE、EC满足的等量关系，并写出推理过程．
11． 如图OA⊥OB，若∠BOC=40°，则∠AOC的度数是（　　）
A．20°B．40°C．50°D．60°
18．汉字“一、中、王、木”它们都是轴对称图形图形，其中“一、中、王”几个字可看成中心对称图形．
8．如图所示，将两个正方形ABCD和正方形CGEF如图所示放置，连接DE、BG．
（1）图中∠DCE+∠BCG=180°；
（2）设△DCE的面积为s1，△BCG的面积为s2，则s1与s2的数量关系为S1=S2；
猜想论证：
如图2所示，将矩形ABCD绕点C按顺时针方向旋转后得到矩形FECG，连接DE、BG，设△DCE的面积为s1，△BCG的面积为s2，猜想s1和s2的数量关系，并加以证明？
如图3所示，在△ABC中，AB=AC=10cm，∠B=30°，把△ABC沿AC翻折得到△AEC，过点A作AD平行CE交BC于点D，在线段CE上存在点△P，使△ABP的面积等于△ACD的面积，请写出CP的长？
15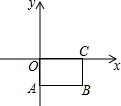．已知，矩形OABC按如图所示的方式建立在平面直角坐标系总，AB=4，BC=2，则点B的坐标为（　　）
A．（4，2）B．（-2，4）C．（4，-2）D．（-4，2）
12．反比例函数y=$\frac{1-5m}{x}$图象上有两点A（x1，y1），B（x2，y2），若x1＜0＜x2，y1＜y2，则m的取值范围是（　　）
A．m＞$\frac{1}{5}$B．m＜$\frac{1}{5}$C．m≥$\frac{1}{5}$D．m≤$\frac{1}{5}$
13．以下列各组数为三角形的三边，能构成直角三角形的是（　　）
A．4，5，6B．1，1，$\sqrt{2}$C．6，8，11D．5，12，23

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网