题目内容
1．若x2+x+a=（x+b）2，则a=$\frac{1}{4}$，b=$\frac{1}{2}$．分析 根据配方法，可以求得a、b的值，注意对应．
解答 解：∵x2+x+$\frac{1}{4}$=（x+$\frac{1}{2}$）2，x2+x+a=（x+b）2，
∴a=$\frac{1}{4}$，b=$\frac{1}{2}$，
故答案为：$\frac{1}{4}$，$\frac{1}{2}$．
点评 本题考查配方法的应用，解题的关键是明确配方法．
练习册系列答案
阅读快车系列答案
相关题目
11．若|x-2|+（x-y-1）2=0，则多项式-y-（x2+2y2）的值为（ ）
| A． | -7 | B． | 5 | C． | -5 | D． | -13 |
6．在平面直角坐标系中．已知A（0，4）．B（-2，0）在坐标轴上确定点P．使△AOP与△AOB相似．则符合条件的点P共有（ ）
| A． | 6个 | B． | 5个 | C． | 4个 | D． | 3个 |
3．
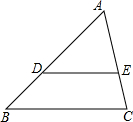如图，DE∥BC，AD：DB=2：1，那么△ADE与△ABC的相似比为（ ）
如图，DE∥BC，AD：DB=2：1，那么△ADE与△ABC的相似比为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{4}$ | D． | 2 |