题目内容
4.将长度为9厘米的木棍截成三段,每段长度均为整数.那么截成的三段木棍能构成等腰三角形的概率是$\frac{2}{7}$.分析 根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率即可得出答案.
解答 解:将长度为9厘米的木棍截成三段,每段长度均为整数,共有1、1、7,1、2、6,1、3、5,1、4、4,2、2、5,2、3、4,3、3、3七种情况,
能构成等腰三角形的有1、4、4,3、3、3两种情况,
则截成的三段木棍能构成等腰三角形的概率是$\frac{2}{7}$,
故答案为:$\frac{2}{7}$.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | (2a2)4=8a6 | B. | a3+a=a4 | C. | (a-b)2=a2-b2 | D. | a2÷a=a |
15.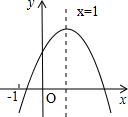 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
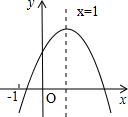 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
13.如果代数式2x-y+1的值为3,那么代数式的4x-2y+5值等于( )
| A. | 11 | B. | 9 | C. | 13 | D. | 7 |
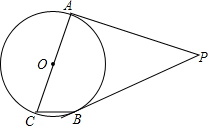 如图:PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB=65°.
如图:PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB=65°.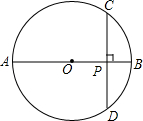 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.