题目内容
5.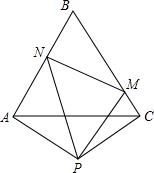 如图,等边△ABC的边长为2,且PA=PC,∠APC=120°,现有∠MPN=60°,将∠MPN绕着P点旋转,使其两边分别与AB、BC交于点N、M.试判断在旋转过程中,△BMN的周长是否发生变化?若不变,请求出周长;若变化,请说明理由.
如图,等边△ABC的边长为2,且PA=PC,∠APC=120°,现有∠MPN=60°,将∠MPN绕着P点旋转,使其两边分别与AB、BC交于点N、M.试判断在旋转过程中,△BMN的周长是否发生变化?若不变,请求出周长;若变化,请说明理由.
分析 先根据等腰三角形的性质和等边三角形的性质求出∠PAC=∠PCB=90°,则把△PCM绕点P逆时针旋转120°得到△PAD,如图,根据旋转的性质得PD=PM,AD=CM,∠PAD=∠PCM=90°,∠MPD=120°,再判断点D在BA的延长线上,则ND=NA+AD=NA+MC,接着证明△PND≌△PNM得到MN=DN,然后利用等线段代换可得△BMN的周长=BA+BC=4.
解答 解:△BMN的周长不变.
∵PA=PC,∠APC=120°,
∴∠PAC=∠PCA=30°,
∵△ABC为等边三角形,
∴∠BAC=∠BCA=60°,
∴∠PAC=∠PCB=90°,
把△PCM绕点P逆时针旋转120°得到△PAD,如图,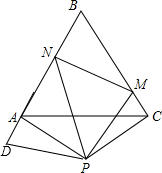
∴PD=PM,AD=CM,∠PAD=∠PCM=90°,∠MPD=120°,
∵∠PAB=90°,
∴点D在BA的延长线上,
∴ND=NA+AD=NA+MC,
∵∠MPN=60°,
∴∠DPN=60°,
在△PND和△PNM中
$\left\{\begin{array}{l}{PN=PN}\\{∠DPN=∠MPN}\\{PD=PM}\end{array}\right.$,
∴△PND≌△PNM,
∴MN=DN,
即MN=NA+MC,
∴,△BMN的周长=BN+MN+BM=BN+NA+MC+BM=BA+BC=2+2=4.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和等边三角形的性质.

练习册系列答案
相关题目
15.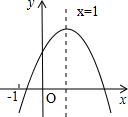 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
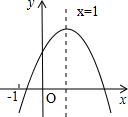 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
13.如果代数式2x-y+1的值为3,那么代数式的4x-2y+5值等于( )
| A. | 11 | B. | 9 | C. | 13 | D. | 7 |
10.计算(-x3)•(-x)3结果正确的是( )
| A. | -x6 | B. | x6 | C. | x5 | D. | -x5 |
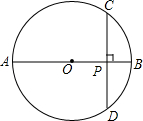 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.