题目内容
3.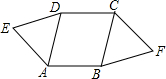 如图,△ADE和△BCF是ABCD外的两个等边三角形,用旋转的知识说明△ADE和△BCF成中心对称.
如图,△ADE和△BCF是ABCD外的两个等边三角形,用旋转的知识说明△ADE和△BCF成中心对称.
分析 连接BE、DF,根据平行四边形的性质得∠1=∠2.再根据,△ADE和△BCF都是等边三角形,得出DE,BF平行且相等,得到平行四边形然后根据旋转的性质的性质推出结论.
解答  证明:连接BE、DF.
证明:连接BE、DF.
∵?ABCD,
∴AD∥BC,AD=BC,
∵AD∥BC,
∴∠1=∠2,
∵三角形ADE是等边三角形,
∴DE=AD,∠3=60°,
∵等边三角形BCF,
∴BC=BF,∠4=60°,
∴DE=BF,
∠1+∠3=∠2+∠4,即∠BDE=∠DBF,
∴DE∥BF,
∴四边形BEDF为平行四边形,
∴点E,A,D绕着点O顺时针旋转180°后与△BCF重合,
∴△ADE和△BCF关于点O成中心对称.
点评 本题考查了旋转的性质,等边三角形的性质和平行四边形的判定和性质,要熟练掌握.

练习册系列答案
相关题目
13.如果代数式2x-y+1的值为3,那么代数式的4x-2y+5值等于( )
| A. | 11 | B. | 9 | C. | 13 | D. | 7 |
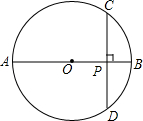 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.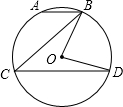 如图,在⊙O中,弦AB∥弦CD,若∠OBD=50°,求∠ABC的度数.
如图,在⊙O中,弦AB∥弦CD,若∠OBD=50°,求∠ABC的度数. 请你利用如图所示的转盘设计一个对双方公平的游戏.
请你利用如图所示的转盘设计一个对双方公平的游戏.