题目内容
2. 如图,长方体的长、宽、高分别是4,3,5,现有绳子从A出发,沿长方形表面到达C处,问绳子最短是$\sqrt{74}$.
如图,长方体的长、宽、高分别是4,3,5,现有绳子从A出发,沿长方形表面到达C处,问绳子最短是$\sqrt{74}$.
分析 把长方体右边的表面展开,连接AC,则AC就是绳子的最短时经过的路径,然后根据勾股定理求解.
解答  解:如图所示,将长方体右边的表面翻折90°(展开),
解:如图所示,将长方体右边的表面翻折90°(展开),
连接AC,显然两点之间线段最短,AC为点A到点C的最短距离,
由勾股定理知:AC2=52+(4+3)2=74,AC=$\sqrt{74}$.
即绳子最短为$\sqrt{74}$.
故答案为:$\sqrt{74}$.
点评 本题考查了平面展开-最短路径问题,勾股定理,知道两点之间线段最短是解题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
13.如果代数式2x-y+1的值为3,那么代数式的4x-2y+5值等于( )
| A. | 11 | B. | 9 | C. | 13 | D. | 7 |
10.计算(-x3)•(-x)3结果正确的是( )
| A. | -x6 | B. | x6 | C. | x5 | D. | -x5 |
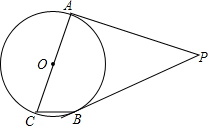 如图:PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB=65°.
如图:PA、PB是⊙O的切线,切点为A、B,AC是直径,若∠P=50°,则∠ACB=65°.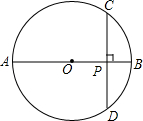 如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,OP=PB+1,求⊙O的半径. 请你利用如图所示的转盘设计一个对双方公平的游戏.
请你利用如图所示的转盘设计一个对双方公平的游戏.