题目内容
13. 某市在旧城改造中.计划在市内一块如图所示的三角形ABC空地上种植草皮以美化环境,已知AB=13米,AD=12米,AD⊥BC,AC=20米.若这种草皮每平方米售价a元.则购买这种草皮至少需要( )
某市在旧城改造中.计划在市内一块如图所示的三角形ABC空地上种植草皮以美化环境,已知AB=13米,AD=12米,AD⊥BC,AC=20米.若这种草皮每平方米售价a元.则购买这种草皮至少需要( )| A. | 126a元 | B. | 150a元 | C. | 156a元 | D. | 300a元 |
分析 根据勾股定理求出线段BD,CD,利用三角形面积公式求出△ABC的面积,再利用草皮购买价=面积×每平方米的单价即可.
解答 解:在RT△ABD中,∵AB=13,AD=12,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
在RT△ADC中,∵AC=20,AD=12,
∴$CD=\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{2{0}^{2}-1{2}^{2}}$=16,
∴BC=BD+CD=21,
∴${S}_{△ABC}=\frac{1}{2}$•BC•AD=$\frac{1}{2}$×21×12=126,
∵这种草皮每平方米售价a元,
∴购买这种草皮至少需要126a元.
故选A.
点评 本题考查勾股定理、三角形面积公式、理解草皮的购买价、每平方米的单价、种值草皮的面积之间的关系是解题的关键.

练习册系列答案
相关题目
4.已知圆锥的母线长为5cm,高为4cm,则这个圆锥的侧面积为( )
| A. | 12πcm2 | B. | 15πcm2 | C. | 20πcm2 | D. | 25πcm2 |
18.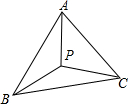 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )| A. | 110° | B. | 130° | C. | 120° | D. | 140° |
 如图,已知直线a,b被直线c所截,且∠5+∠2=180°,可以判定直线a∥b吗?试着用不同的方法说明你的结论.
如图,已知直线a,b被直线c所截,且∠5+∠2=180°,可以判定直线a∥b吗?试着用不同的方法说明你的结论. 在同一平面直角坐标系中,函数y1=$\frac{1}{2}$x与y2=$\frac{2}{x}$的图象如图所示,试利用图象回答下列问题:
在同一平面直角坐标系中,函数y1=$\frac{1}{2}$x与y2=$\frac{2}{x}$的图象如图所示,试利用图象回答下列问题: