Question

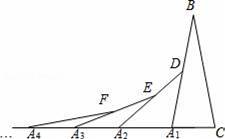
如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BEDF是菱形，且EF=AE+FC，则边BC的长为　　　　　　．

Answer 1

　3　．

 

【考点】矩形的性质；菱形的性质．

【分析】根据矩形的性质和菱形的性质得∠ABE=∠EBD=∠DBC=30°，AB=BO=3，因为四边形BEDF是菱形，所以可求出BE，AE，进而可求出BC的长．

【解答】解：∵四边形ABCD是矩形，四边形BEDF是菱形，

∴∠A=90°，AD=BC，DE=BF，OE=OF，EF⊥BD，∠EBO=FBO，

∴AE=FC．又EF=AE+FC，

∴EF=2AE=2CF，又EF=2OE=2OF，AE=OE，

∴△ABE≌OBE，

∴∠ABE=∠OBE，

∴∠ABE=∠EBD=∠DBC=30°，

∴BE=，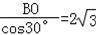

∴BF=BE=2，

∴CF=AE=，

∴BC=BF+CF=3，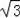

故答案为：3．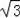

【点评】本题考查了矩形的性质、菱形的性质以及在直角三角形中30°角所对的直角边时斜边的一半，解题的关键是求出∠ABE=∠EBD=∠DBC=30°．