题目内容
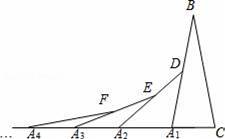
如图,在第1个△A1BC中,∠B=20°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第5个三角形中以A5为顶点的内角度数是 .

5° .
【考点】等腰三角形的性质.
【专题】规律型.
【分析】先根据等腰三角形的性质求出∠BA1C的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律即可得出第n个三角形中以An为顶点的内角度数.
【解答】解:∵在△CBA1中,∠B=20°,A1B=CB,
∴∠BA1C=
 =80°,
=80°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=
 ∠BA1C=
∠BA1C=
 ×80°;
×80°;
同理可得,
∠EA3A2=(
 )2×80°,∠FA4A3=(
)2×80°,∠FA4A3=(
 )3×80°,
)3×80°,
∴第n个三角形中以An为顶点的内角度数是(
 )n﹣1×80°.
)n﹣1×80°.
∴第5个三角形中以A5为顶点的内角度数为: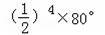
 =5°,
=5°,
故答案为:5°.
【点评】本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠DA2A1,∠EA3A2及∠FA4A3的度数,找出规律是解答此题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目



 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.

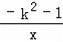
 的图象上.下列结论中正确的是( )
的图象上.下列结论中正确的是( )
 = .
= .
 ,当半圆O旋转至与△ABC的边相切时,线段BD= .
,当半圆O旋转至与△ABC的边相切时,线段BD= .

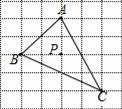


 是整数,则满足条件的最小正整数n为( )
是整数,则满足条件的最小正整数n为( )
