题目内容
在矩形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )


A.2和3 B.3和2 C.4和1 D.1和4
B【考点】矩形的性质.
【分析】先根据角平分线及矩形的性质得出∠BAE=∠AEB,再由等角对等边得出BE=AB,从而求出EC的长.
【解答】解:∵AE平分∠BAD交BC边于点E,
∴∠BAE=∠EAD,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=5,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE=3,
∴EC=BC﹣BE=5﹣3=2,
故选:B.
【点评】本题主要考查了角平分线、矩形的性质及等腰三角形的判定,根据已知得出∠BAE=∠AEB是解决问题的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目

 =±
=±
 B.
B.
 =1
=1

 =﹣3 D.
=﹣3 D.
 =
=

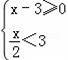
 的所有整数解之和是( )
的所有整数解之和是( )


 (
(
 ﹣
﹣

 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.


 是整数,则满足条件的最小正整数n为( )
是整数,则满足条件的最小正整数n为( )