题目内容
9.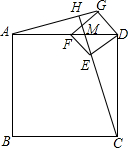 如图,若四边形ABCD、四边形GFED都是正方形,AD=4,$DE=\sqrt{2}$,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为$\frac{4}{3}\sqrt{10}$.
如图,若四边形ABCD、四边形GFED都是正方形,AD=4,$DE=\sqrt{2}$,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为$\frac{4}{3}\sqrt{10}$.
分析 先过点E作EQ⊥CD于Q,构造等腰直角三角形DEG,并求得其直角边长,再根据EQ∥MD,运用平行线分线段成比例定理,求得MD的长,最后在直角三角形CDM中根据勾股定理求得斜边CM的长.
解答 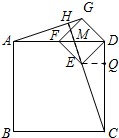 解:过点E作EQ⊥CD于Q,则∠EQD=90°,
解:过点E作EQ⊥CD于Q,则∠EQD=90°,
∵正方形DEFG中∠EDF=45°,正方形ABCD中∠ADC=90°,
∴∠EDQ=90°-45°=45°,
∴△DEQ是等腰直角三角形,
∵DE=$\sqrt{2}$,
∴EQ=DQ=1,
又∵AD=4=CD,
∴CQ=4-1=3,
∵EQ∥MD,
∴$\frac{DM}{QE}$=$\frac{DC}{QC}$,即$\frac{DM}{1}$=$\frac{4}{3}$,
∴DM=$\frac{4}{3}$,
∴直角三角形CDM中,CM=$\sqrt{{4}^{2}+(\frac{4}{3})^{2}}$=$\frac{4}{3}\sqrt{10}$.
故答案为:$\frac{4}{3}\sqrt{10}$
点评 本题以图形旋转为背景,考查了正方形的性质以及勾股定理,解决问题的关键是作辅助线,运用平行线分线段成比例定理进行求解.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
18.已知点P(a,b)是反比例函数$y=\frac{4}{x}$图象上异于点(-2,-2)的一个动点,则$\frac{1}{2+a}+\frac{1}{2+b}$的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 4 |
19.顺次连接一个矩形各边的中点,得到的四边形一定是( )
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
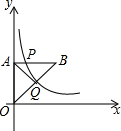 如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,
如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y=$\frac{k}{x}$的图象交斜边OB于点Q,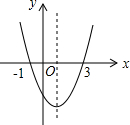 图为二次函数y=ax2+bx+c的图象,给出下列说法:
图为二次函数y=ax2+bx+c的图象,给出下列说法:
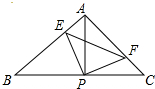 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF=$\frac{1}{2}$S△ABC,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④S四边形AEPF=$\frac{1}{2}$S△ABC,当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确有 ( ) 如图,已知在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,给出下列结论:
如图,已知在正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,给出下列结论: