题目内容
8. 如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为6$\sqrt{3}$米,斜坡BC的坡度i=1:$\sqrt{3}$.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.
如图山坡上有一根旗杆AB,旗杆底部B点到山脚C点的距离BC为6$\sqrt{3}$米,斜坡BC的坡度i=1:$\sqrt{3}$.小明在山脚的平地F处测量旗杆的高,点C到测角仪EF的水平距离CF=1米,从E处测得旗杆顶部A的仰角为45°,旗杆底部B的仰角为20°.(1)求坡角∠BCD;
(2)求旗杆AB的高度.
(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
分析 (1)根据坡度i与坡角α之间的关系为:i=tanα进行计算;
(2)根据余弦的概念求出CD,根据正切的概念求出AG、BG,计算即可.
解答 解:(1)∵斜坡BC的坡度i=1:$\sqrt{3}$,
∴tan∠BCD=$\frac{BD}{DC}$=$\frac{\sqrt{3}}{3}$,
∴∠BCD=30°;
(2)在Rt△BCD中,CD=BC×cos∠BCD=6$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=9,
则DF=DC+CF=10(米),
∵四边形GDFE为矩形,
∴GE=DF=10(米),
∵∠AEG=45°,
∴AG=DE=10(米),
在Rt△BEG中,BG=GE×tan∠BEG=10×0.36=3.6(米),
则AB=AG-BG=10-3.6=6.4(米).
答:旗杆AB的高度为6.4米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题和坡度坡角问题,掌握仰角俯角的概念和坡度坡角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
18.下列四个命题中是真命题的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 实数与数轴上的点是一一对应的 | |
| D. | 如果一个数能被2整除,那么它也能被4整除 |
19. 如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
 如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )
如图,在平行四边形ABCD中,∠A+∠C=220°,则∠B的度数是( )| A. | 60° | B. | 70° | C. | 100° | D. | 120° |
16. 如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在此位置上,使AB固定,逆时针转动AD.则关于?ABCD面积变化情况叙述正确的是( )
如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在此位置上,使AB固定,逆时针转动AD.则关于?ABCD面积变化情况叙述正确的是( )
 如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在此位置上,使AB固定,逆时针转动AD.则关于?ABCD面积变化情况叙述正确的是( )
如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在此位置上,使AB固定,逆时针转动AD.则关于?ABCD面积变化情况叙述正确的是( )| A. | 先变大,再变小 | B. | 先变小,再变大 | ||
| C. | 保持不变 | D. | 转动过程中,?ABCD面积没有最大值 |
13.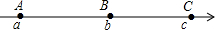 如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,则下列关系正确的是( )
如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,则下列关系正确的是( )
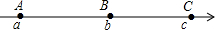 如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,则下列关系正确的是( )
如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,则下列关系正确的是( )| A. | a+c=2b | B. | b>c | C. | c-a=2(a-b) | D. | a=c |
 小李在参与“设计遮阳篷”的活动中,测得自己家的窗户高AB为1.5米,上网了解到本地区太阳光与地面的最大夹角∠DAE约为73°,最小夹角∠DBF约为28°,请根据所提供的信息,计算出直角形遮阳篷BCD中BC和CD的长度分别为多少米?(结果精确到0.1,参考数据:sin73°≈0.96,cos73°≈0.29,tan73°=≈3.27,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
小李在参与“设计遮阳篷”的活动中,测得自己家的窗户高AB为1.5米,上网了解到本地区太阳光与地面的最大夹角∠DAE约为73°,最小夹角∠DBF约为28°,请根据所提供的信息,计算出直角形遮阳篷BCD中BC和CD的长度分别为多少米?(结果精确到0.1,参考数据:sin73°≈0.96,cos73°≈0.29,tan73°=≈3.27,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53) 如图,直线y=kx+b经过点A(-1,0)和B(3,-1)两点,则不等式x-4<kx+b≤0的解为3≤x<4.
如图,直线y=kx+b经过点A(-1,0)和B(3,-1)两点,则不等式x-4<kx+b≤0的解为3≤x<4.